Next: Some experimental results Up: Uncalibrated Stereo Correspondence Previous: The Scott and Longuet-Higgins

Stereo matching by SVD

Let us now consider the case of real images pairs, and the problem of matching across points of interest (e.g. corners). Actual point feature detectors are unstable and it is reasonable to expect that some points that appear in one image do not show up in the other ( rogue points ).

Rogue points cause lots of ambiguous, equally good matching possibilities in the space of pairings, and the sole proximity used to build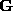 in Equation ( 1 ) does not have enough ``character'' to discriminate amongst them. As a consequence, only a handful of features are safely in one-to-one correspondence with others (also pointed out in [ 8 ]).

   
Figure 1: LEFT: The SVD method applied with G as in Eqn. ( 1 ) leaves out many points due to ambiguities caused by rogue points. RIGHT: The SVD method applied with just point correlation yield non-sense results.

Only a few experiments are needed to realize the entity of this problem. Figure 1 -left shows how only few corners (cf. with Figure 2 ) are found in 1:1 correspondence; a much larger number of highly-correlated corners (not shown) are left out because rogue points cannot be told apart from good ones just from their spatial location. This behavior can be summarized by saying that the Scott and Longuet-Higgins algorithm does not embed the feature similarity principle , so dear to most stereo correspondence approaches.

Obviously, this behavior calls for the use of some local measurements to quantify feature similarity, such as the normalized (cross) correlation between gray level patches about the features.

If we represent two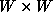 areas centered on features 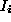and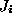 as two 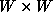arrays of pixel intensities 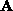and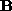 , respectively, the normalized correlation is defined as 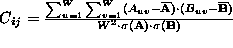where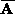 ( 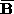) is the average and 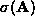( 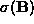) the standard deviation of all the elements of 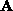( 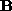). 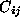varies from -1 for completely uncorrelated patches to 1 for identical patches.

One way of including this correlation information into the proximity matrix is to transform the elements of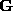 as follows:
 
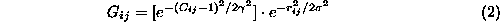
where term is bracket is a Gaussian-weighted function of the correlation in which determines how quickly its values decreases with a diminishing ( 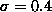throughout the paper).

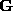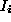This new correspondence strength can be seen as a correlation-weighted proximity . It is easy to see that the elements of still range from 0 to 1 and, as in Equation ( 1 ), the closer and the more correlated two features and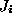 are, the higher 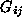is going to be.

This new correspondence strength now embodies the similarity between features and is therefore much more selective than just proximity as in Equation ( 1 ). In some ways, by applying the algorithm with the said correlation-weighted G we obtain a minimum overall distance mapping that is still complying to the proximity and uniqueness principles but also under the constraint of similarity .

   
Figure 2: SVD matching with correspondence strength as in Eqn. ( 2 ). Disparities are overlaid onto the left image and matching corners are shown in the right one. Notice how the method managed to find the correct correspondences in difficult areas such as in the back of the stapler. (Images courtesy of INRIA)

Figure 2 -left shows the matches obtained by this method for the same image as of Figure 1 -left. It can be seen that a considerably higher number of 1:1 matches has been found. In other examples (not shown here) many bad pairings were also replaced by correct ones.

Next section discusses this experiment and others in further detail to show the effectiveness of the method.