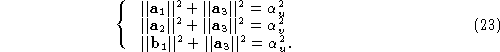Next:
5 Solving for the
Up:
Rectification with unconstrained stereo
Previous:
3 The rectification transformation
To compute the rectifying projection matrices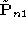 and
and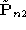 , we set up a linear, homogeneous system of equations formed by the
constraints sufficient to guarantee rectification [
1
], and incorporate explicitly quadratic constraints on the entries of
, we set up a linear, homogeneous system of equations formed by the
constraints sufficient to guarantee rectification [
1
], and incorporate explicitly quadratic constraints on the entries of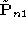 and
and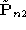 to ensure a nontrivial solution. The constrained system and its
equations are detailed in this section. In the following, we shall write
to ensure a nontrivial solution. The constrained system and its
equations are detailed in this section. In the following, we shall write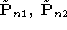 as follows:
as follows:
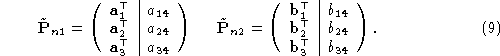
Projection matrices are defined up to a scale factor. The common choice
to block the latter is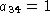 and
and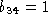 [
1
], unfortunately, brings about two problems: first, the intrinsic
parameters become dependent on the choice of the world coordinate system
[
5
]; second, the resulting projection matrices do not satisfy the
conditions guaranteeing that meaningful calibration parameters can be
extracted from their entries of the matrices [
4
], that is (for example for
[
1
], unfortunately, brings about two problems: first, the intrinsic
parameters become dependent on the choice of the world coordinate system
[
5
]; second, the resulting projection matrices do not satisfy the
conditions guaranteeing that meaningful calibration parameters can be
extracted from their entries of the matrices [
4
], that is (for example for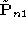 ),
),
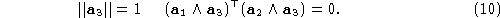
To obviate the problems mentioned, we enforce
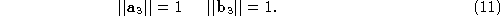
The second equation in (
10
) and its equivalent for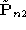 are actually implied by the system defining our algorithm (proof omitted
for reasons of space).
are actually implied by the system defining our algorithm (proof omitted
for reasons of space).
The optical centers of the rectified projections,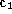 and
and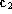 , must be the same as those of the original projections:
, must be the same as those of the original projections:
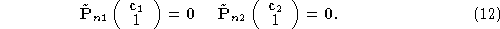
Eq. (
12
) gives six linear constraints:
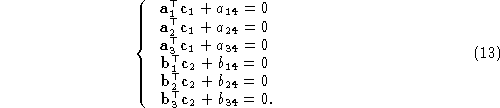
The two rectified projections must share the same focal plane, i.e.
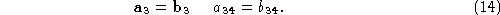
The vertical coordinate of the projection of a 3-D point onto the
rectified retinal plane must be the same in both image, i.e:
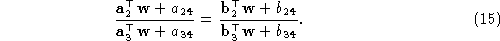
Using Eq. (
14
) we obtain the constraints
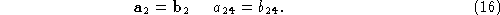
Notice that the equations written to this point are sufficient to
guarantee rectification (indeed some authors stop here, e.g. [
1
]),
but not a unique solution
: the orientation of the rectified retinal plane and the intrinsic
parameters are still free. Our algorithm constrains these quantities
explicitly, as follows.
We choose the rectified focal planes to be parallel to the intersection
of the two original focal planes, i.e.
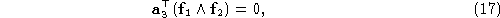
where and
and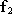 are the third rows of
are the third rows of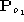 and
and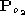 respectively. Notice that the dual equation
respectively. Notice that the dual equation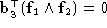 is redundant thanks to Eq. (
14
).
is redundant thanks to Eq. (
14
).
The intersections of the retinal plane with the planes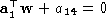 and
and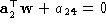 correspond to the
v
and
u
axes, respectively, of the retinal reference frame. As this reference
frame to be orthogonal, the planes must be perpendicular, hence, using
Eq. (
16
),
correspond to the
v
and
u
axes, respectively, of the retinal reference frame. As this reference
frame to be orthogonal, the planes must be perpendicular, hence, using
Eq. (
16
),
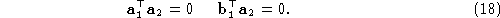
Given a full-rank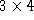 matrix satisfying constraints (
10
), the principal point
matrix satisfying constraints (
10
), the principal point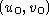 is given by [
4
]:
is given by [
4
]:
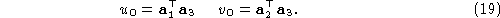
We set the two principal points to (0,0) and use Eqs. (
14
) and (
16
) to obtain the constraints
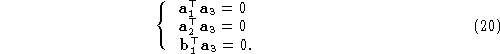
The horizontal and vertical focal lengths in pixels, respectively, are
given by
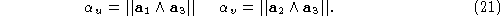
By setting the values of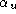 and
and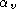 , for example, to the values extracted from
, for example, to the values extracted from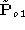 , we obtain the constraints
, we obtain the constraints
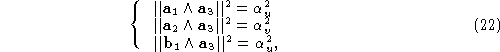
which, by virtue of the equivalence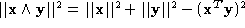 and Eq. (
20
), can be rewritten as
and Eq. (
20
), can be rewritten as
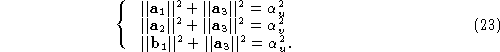



Next:
5 Solving for the
Up:
Rectification with unconstrained stereo
Previous:
3 The rectification transformation
Adrian F Clark
Wed Jul 23 16:48:44 BST 1997
 and
and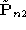 , we set up a linear, homogeneous system of equations formed by the
constraints sufficient to guarantee rectification [
1
], and incorporate explicitly quadratic constraints on the entries of
, we set up a linear, homogeneous system of equations formed by the
constraints sufficient to guarantee rectification [
1
], and incorporate explicitly quadratic constraints on the entries of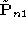 and
and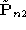 to ensure a nontrivial solution. The constrained system and its
equations are detailed in this section. In the following, we shall write
to ensure a nontrivial solution. The constrained system and its
equations are detailed in this section. In the following, we shall write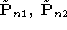 as follows:
as follows:


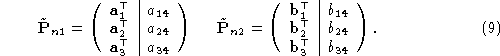
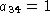 and
and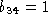 [
[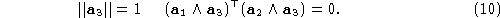
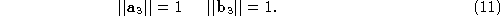
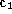 and
and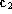 , must be the same as those of the original projections:
, must be the same as those of the original projections: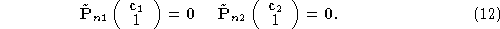
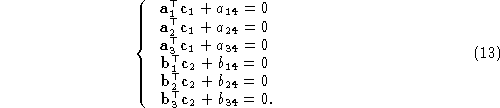
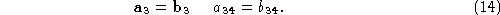
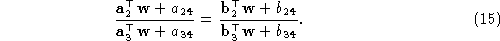
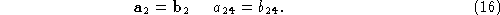
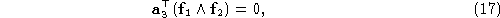
 and
and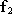 are the third rows of
are the third rows of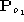 and
and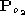 respectively. Notice that the dual equation
respectively. Notice that the dual equation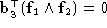 is redundant thanks to Eq. (
is redundant thanks to Eq. (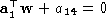 and
and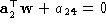 correspond to the
v
and
u
axes, respectively, of the retinal reference frame. As this reference
frame to be orthogonal, the planes must be perpendicular, hence, using
Eq. (
correspond to the
v
and
u
axes, respectively, of the retinal reference frame. As this reference
frame to be orthogonal, the planes must be perpendicular, hence, using
Eq. (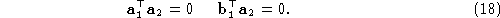
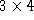 matrix satisfying constraints (
matrix satisfying constraints (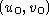 is given by [
is given by [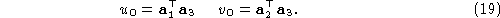
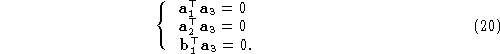
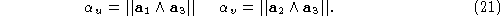
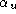 and
and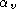 , for example, to the values extracted from
, for example, to the values extracted from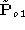 , we obtain the constraints
, we obtain the constraints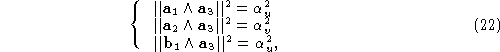
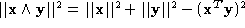 and Eq. (
and Eq. (