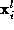 , the associated measurement vector for that pixel at resolution level
l
. We define a label set
, the associated measurement vector for that pixel at resolution level
l
. We define a label set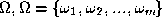 , which contains all possible labels of the image for
m
possible categories. Thus, each pixel
i
has label
, which contains all possible labels of the image for
m
possible categories. Thus, each pixel
i
has label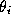 that can take on values from
that can take on values from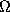 .
.
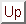

The problem of multiscale probabilistic labelling of the input image
using a set of blurred versions of the image can be stated as follows.
Let
l
indicate the levels of coarsening with
l
= 1,...,
L
, representing the levels from full resolution to the coarsest level.
Let
i
,
i
=1,...,
N
be a pixel and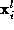 , the associated measurement vector for that pixel at resolution level
l
. We define a label set
, the associated measurement vector for that pixel at resolution level
l
. We define a label set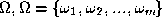 , which contains all possible labels of the image for
m
possible categories. Thus, each pixel
i
has label
, which contains all possible labels of the image for
m
possible categories. Thus, each pixel
i
has label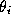 that can take on values from
that can take on values from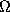 .
.
We wish to choose for pixel
i
the most probable label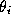 given all the available information. In other words we wish to set:
given all the available information. In other words we wish to set:
For simplicity and clarity of exposition we shall restrict ourselves in considering only two successive levels of resolution l and l +1. Then, using Bayes's Rule:
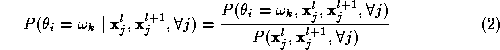
We can expand the terms in the numerator and the denominator by applying
the theorem of total probability:
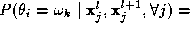
The joint probability that appears in Equation 3 can be factorised as follows:
As we try to emulate here perceptual segmentation, we can imagine that due to causality, measurements obtained at level l +1 (the coarser level) can not possibly depend on measurements obtained at level l . Thus, the first factor on the right hand side of Equation 4 can be simplified as follows:
We also expect that the measurement concerning a certain pixel depends on the identity of that pixel alone and on nothing else. Therefore, we can further write:
where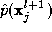 is the prior probability of measurements
is the prior probability of measurements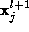 to arise, and
to arise, and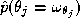 is the prior probability of label
is the prior probability of label .
.
Now consider the second factor on the right hand side of Equation 4 :
We can further expand the second term on the right hand side of Equation 7 to write:
For the same reasons explained earlier, we expect that the measurement obtained for a particular object depends on the identity of the object itself and on nothing else. Thus, all factors on the right hand side of Equation 8 , except the last one, can be simplified to express dependence only on the identity of the object they refer to. The last factor is the joint probability of a certain label assignment to arise. So we have:
Now by substituting from Equations 6 and 9 in Equation 4 :
Then, upon substitution in Equation 3 :
where
In the above expression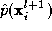 is independent of the summation indices and cancels in the numerator and
denominator. Therefore, the above expression further simplifies and
gives the following formula for the labelling of a pixel from one level
to the next:
is independent of the summation indices and cancels in the numerator and
denominator. Therefore, the above expression further simplifies and
gives the following formula for the labelling of a pixel from one level
to the next:
At the finest resolution equations 1 and 13 give the final segmentation result. The latter expression states that the probability of a certain pixel to have a certain label is equal to the product of the probability of the values of the measurements concerning the pixel to arise given the identity of the pixel, times the probability of the pixel to have this identity given the measurements concerning it at coarser resolutions, times a factor that expresses the contextual information. The denominator in the above formula is simply a normalising constant. The contextual information factor not only contains the product of measurement probabilities to arise given pixel identities, times probabilities of pixel identities given coarser measurements summed over all other pixels, but also the probability of a particular combination of pixel identities to arise. In the next section the meaning of all these factors will become clearer.


Dr. Majid Mirmehdi