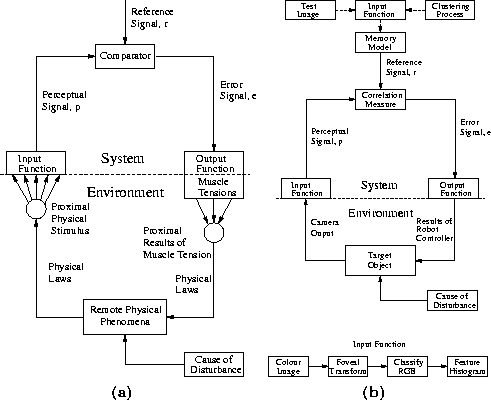
Figure: a) General model of a feedback control system and its local environment. (Reproduced with permission from Powers [ 7 ], p. 61), b) Schematic model of feedback control vision system under development.


A schematic diagram of the lowest level of the system under development is shown in figure 1 b. Each component is briefly described below with the foveal fixation measure discussed in more detail.

Figure:
a) General model of a feedback control system and its local environment.
(Reproduced with permission from Powers [
7
], p. 61), b) Schematic model of feedback control vision system under
development.
The representation of objects and scene used is simply that of a count, or histogram, of features relevant to a target. In the current system colour features are used mainly because they can be processed relatively quickly compared to other types of features. It is intended, however, that the scheme can be extended to any kind of feature as the measure is dependent upon the feature count and not the feature type . The main rationale for a histogram of features is indicated in the later discussion on pixel count , however this type of simple computation (addition) and representation (activations) is consistent with what is possible with neurons or groups of neurons.
The current, or training, image is converted into the foveal representation by applying a log-polar transformation [ 9 ]. To avoid the washing-out of colours in an area of pixels, the method used for deriving a single colour from the uniform image is to take the modal value of the set of colours as oppose to the average of the area. The RGB feature vectors at each pixel in the log-polar image are then adjusted for intensity by,

where G is the gamma value of the camera and c is the red, green or blue values.
Within the learning process, performed on the training image, the feature vectors are clustered according to a k-means clustering process resulting in a reduced set of vectors (the clusters means) that represent the features specific to the model object. The histograms for the model and the scene are produced by counting how many features from the foveal RGB image fall within each cluster, for the set of clusters representing the target object. For example, at each pixel the RGB vector is adjusted for intensity and then compared with each of the ten, say, cluster means. If it is within three standard deviations of a particular distribution it is said to belong to that cluster and the histogram is incremented appropriately.
The philosophy of this system is not to identify objects in a scene but to model the general behaviour by which an animate system can position itself relative to a specified object. Such behaviour could, however, be used as a mechanism for providing an identification system with the best available information.
The behaviour is dependent upon a measure of how close the current view is to that desired. The measure is derived from a comparison between the model and scene histograms. Such correlation methods include the sum of squared distances and the Bhattacharya distance. Results presented in section 6 use the former method.
The basis for the motivation of behaviour and the measure of fixation is derived from a very simple property of the foveal representation, referred to as pixel count [ 12 ].
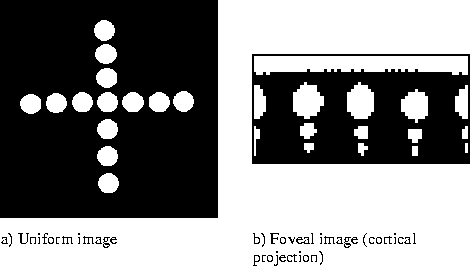
Figure 2:
Demonstration of the property of maximum pixel count at the fovea.
Figure 2 demonstrates this property on a simple circular shape. Figure 2 a shows a standard, uniform image with a white circle in a number of different positions. Note that wherever the circle is in the image its size is the same, i.e. the pixel count is constant. Figure 2 b is the foveal representation of the same scene with the foveal point centred on the uniform image. Each row in the foveal representation (in this rectangular format, it is also known as the cortical projection due to the similarity with the structure of the visual cortex) represents a ring of pixel areas around the centre of the uniform image. The further the ring is from the centre, the larger the pixel area. Each area of pixels, in the uniform image, maps to one pixel in the cortical projection resulting in an image of decreasing resolution for each subsequent row from the fovea (the top row). Now notice what happens to the same circle as it moves away from the fovea. At the fovea the circle has a maximum pixel count (the band of white at the top of the foveal image) which gets smaller and smaller as the shape moves away from the centre. Given this property it is possible to determine when the circle is fixated, with a controlling mechanism that adjusts position and maximises the pixel count. Incidentally, this method equates to finding the centroid for an arbitrarily shaped figure.
The scheme can be extended slightly to operate with a specific view of an object, which equates to a specific pixel count. So the current view would be correct when the current pixel count is the same as that of the model.

This equation simply states that the error signal is the reference pixel count, , minus the current, or perceptual, pixel count, . This difference can be used to drive the fixation to the correct point. The real world example in section reffixmeas uses this principle, but instead of just counting one binary feature the input function counts multiple colour features corresponding to a particular object.
The output function, or controller, relates the error signal to the direction of movement of the artificial animate system in three dimensions. Within this control-based scheme it is not necessary to compute the specific values of the position parameters but to change them in such a way that the error signal is minimised and a specific input is realised. It is proposed that the automatic control of the sensor can be achieved by a simple gradient descent technique.


Rupert J Young