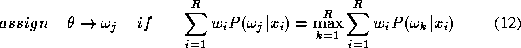Next:
Error sensitivity
Up:
Weighting Factors in Multiple
Previous:
Introduction
Consider an image labelling problem where object Z is to be assigned to
one of
m
possible semantic categories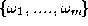 . Let us assume that we have R experts each representing the given
object by a distinct measurement vector. Denote the measurement vector
used by the i-th expert by
. Let us assume that we have R experts each representing the given
object by a distinct measurement vector. Denote the measurement vector
used by the i-th expert by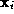 . In the measurement space each class
. In the measurement space each class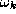 is modelled by the probability density function
is modelled by the probability density function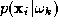 and its a priori probability of occurrence is denoted
and its a priori probability of occurrence is denoted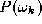 . We shall consider the models to be mutually exclusive which means that
only one model can be associated with each object.
. We shall consider the models to be mutually exclusive which means that
only one model can be associated with each object.
According to the Bayesian theory, given measurements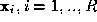 , the object,
Z
, should be assigned to class
, the object,
Z
, should be assigned to class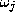 , i.e. its label
, i.e. its label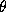 should assume value
should assume value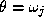 , provided the aposteriori probability of that interpretation is
maximum, i.e.
, provided the aposteriori probability of that interpretation is
maximum, i.e.
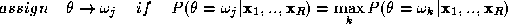
Let us rewrite the aposteriori probability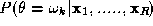 using the Bayes theorem. We have
using the Bayes theorem. We have
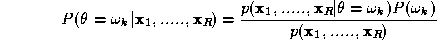
where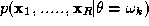 is the class conditional joint probability density and
is the class conditional joint probability density and is the unconditional measurement joint probability density. The latter
can be expressed in terms of the conditional measurement distributions
as
is the unconditional measurement joint probability density. The latter
can be expressed in terms of the conditional measurement distributions
as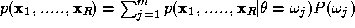 and therefore, in the following, we can concentrate only on the
numerator terms of (
2
).
and therefore, in the following, we can concentrate only on the
numerator terms of (
2
).
Since the representations used by the experts are distinct, it may be
reasonable to assume that measurements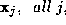 will be conditionally statistically independent, i.e
will be conditionally statistically independent, i.e
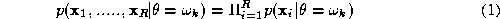
where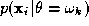 is the measurement process model of the i-th representation.
Substituting from (
1
) into (
2
) we find
is the measurement process model of the i-th representation.
Substituting from (
1
) into (
2
) we find
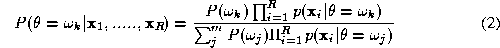
and using (
2
) in (
2
) we obtain the decision rule
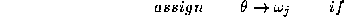
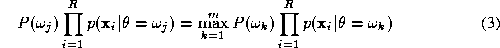
or in terms of the aposteriori probabilities yielded by the respective
experts
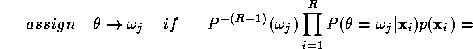
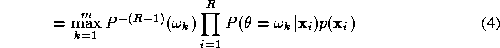
The decision rule (
4
) quantifies the likelihood of a hypothesis by combining the aposteriori
probabilities generated by the individual experts by means of a product
rule. It is effectively a severe rule of fusing the expert outputs as it
is sufficient for a single recognition engine to inhibit a particular
interpretation by outputting a close to zero probability for it. We
shall adopt the approach used in [
2
] to show that under certain assumptions this severe rule can be
developed into a benevolent information fusion rule which has the form
of a sum. Let us express the product of the aposteriori probabilities
and mixture densities on the right hand side of (
4
)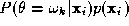 as
as
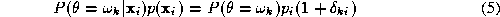
where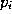 is a nominal reference value of the mixture density
is a nominal reference value of the mixture density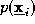 . A suitable choice of
. A suitable choice of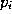 is for instance
is for instance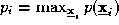 . Substituting (
5
) for the aposteriori probabilities in (
4
) we find
. Substituting (
5
) for the aposteriori probabilities in (
4
) we find
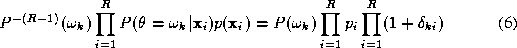
If we expand the product and neglect any terms of second and higher
order we can approximate the right hand side of (
6
) as
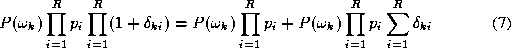
Substituting (
7
) and (
5
) into (
4
) and eliminating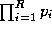 we obtain a sum decision rule
we obtain a sum decision rule
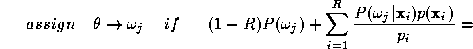
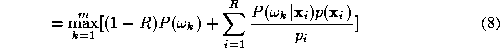
This approximation will be valid provided that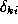 satisfies
satisfies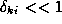 . It can be easily established that this condition will be satisfied if
. It can be easily established that this condition will be satisfied if
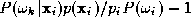 will be small in absolute value sense. Note that this condition will
hold when the amount of information about class identity of the object
gained by observing
will be small in absolute value sense. Note that this condition will
hold when the amount of information about class identity of the object
gained by observing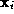 is small and the observation is representative for the distinction of
is small and the observation is representative for the distinction of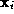 which means that
which means that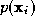 will be close to the reference value
will be close to the reference value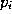 . However, whatever approximation error is introduced when the
conditions do not hold, we shall see later that the adoption of the
approximation has some other benefits which will justify even the
introduction of relatively gross errors at this step.
. However, whatever approximation error is introduced when the
conditions do not hold, we shall see later that the adoption of the
approximation has some other benefits which will justify even the
introduction of relatively gross errors at this step.
Before proceeding any further, it may be pertinent to ask, why we did
not cancel out the unconditional probability density functions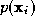 from the decision rule. The main reasons is that this term conveys very
useful information about the confidence of the expert in the observation
made. It is clear that an object representation for which the value of
the probability density is very small for all the classes will be an
outlier and should not be classified by the respective expert. By
retaining this information, the sum information fusion rule will
automatically control the influence of such outliers on the final
decision. In other words, the expert fusion rule in (
8
) is a weighted average rule where the weights reflect the confidence in
the soft decision values computed by the individual experts. Thus our
decision rule (
8
) can be expressed as
from the decision rule. The main reasons is that this term conveys very
useful information about the confidence of the expert in the observation
made. It is clear that an object representation for which the value of
the probability density is very small for all the classes will be an
outlier and should not be classified by the respective expert. By
retaining this information, the sum information fusion rule will
automatically control the influence of such outliers on the final
decision. In other words, the expert fusion rule in (
8
) is a weighted average rule where the weights reflect the confidence in
the soft decision values computed by the individual experts. Thus our
decision rule (
8
) can be expressed as
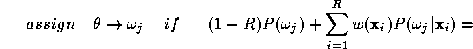
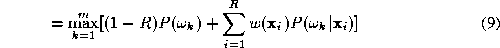
The main practical difficulty with the weighted average expert opinion
combiner as specified in (
9
) is that not all experts will have the inner capability to output such
information. For instance, it would not be provided by a multilayer
perceptron and many other classification methods. We shall therefore
limit our objectives somewhat and identify the weights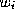 which will reflect the relative confidence in the experts in
expectation. This can be done easily by selecting weight values by means
of minimising the empirical classification error count produced by the
decision rule
which will reflect the relative confidence in the experts in
expectation. This can be done easily by selecting weight values by means
of minimising the empirical classification error count produced by the
decision rule
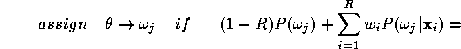
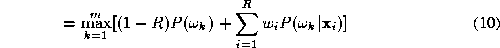
in which the data dependence of the weights has been suppressed. In
other words we find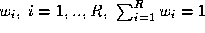 such that
such that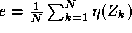 where
where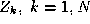 is the k-th training sample and
is the k-th training sample and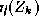 takes values
takes values
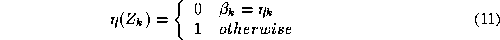
is minimised. In (
11
),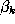 is the true class label of object
is the true class label of object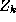 and
and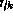 is the class label assigned to it by the decision rule (
10
). The optimisation can easily be achieved by an exhaustive search
through the weight space.
is the class label assigned to it by the decision rule (
10
). The optimisation can easily be achieved by an exhaustive search
through the weight space.
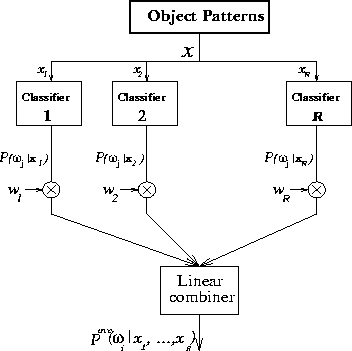
Figure 1:
Weighted averaging fusion of multiple expert opinions.
For equal a priori class probabilities the decision rule (
10
) simplifies to:
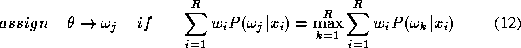
The weighted averaging combiner is schematically represented in Figure
1
.



Next:
Error sensitivity
Up:
Weighting Factors in Multiple
Previous:
Introduction
S Ali Hojjatoleslami
Tue Jul 15 17:20:44 BST 1997
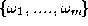 . Let us assume that we have R experts each representing the given
object by a distinct measurement vector. Denote the measurement vector
used by the i-th expert by
. Let us assume that we have R experts each representing the given
object by a distinct measurement vector. Denote the measurement vector
used by the i-th expert by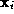 . In the measurement space each class
. In the measurement space each class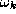 is modelled by the probability density function
is modelled by the probability density function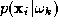 and its a priori probability of occurrence is denoted
and its a priori probability of occurrence is denoted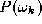 . We shall consider the models to be mutually exclusive which means that
only one model can be associated with each object.
. We shall consider the models to be mutually exclusive which means that
only one model can be associated with each object.


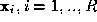 , the object,
Z
, should be assigned to class
, the object,
Z
, should be assigned to class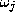 , i.e. its label
, i.e. its label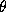 should assume value
should assume value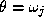 , provided the aposteriori probability of that interpretation is
maximum, i.e.
, provided the aposteriori probability of that interpretation is
maximum, i.e.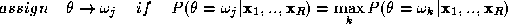
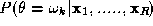 using the Bayes theorem. We have
using the Bayes theorem. We have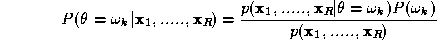
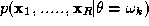 is the class conditional joint probability density and
is the class conditional joint probability density and is the unconditional measurement joint probability density. The latter
can be expressed in terms of the conditional measurement distributions
as
is the unconditional measurement joint probability density. The latter
can be expressed in terms of the conditional measurement distributions
as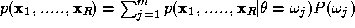 and therefore, in the following, we can concentrate only on the
numerator terms of (
and therefore, in the following, we can concentrate only on the
numerator terms of (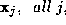 will be conditionally statistically independent, i.e
will be conditionally statistically independent, i.e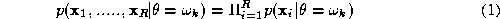
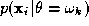 is the measurement process model of the i-th representation.
Substituting from (
is the measurement process model of the i-th representation.
Substituting from (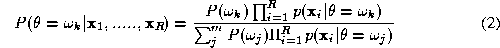
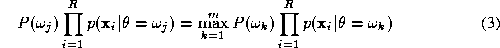
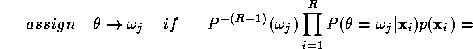
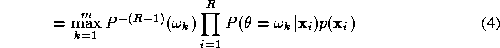
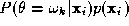 as
as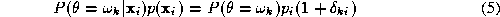
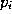 is a nominal reference value of the mixture density
is a nominal reference value of the mixture density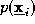 . A suitable choice of
. A suitable choice of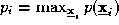 . Substituting (
. Substituting (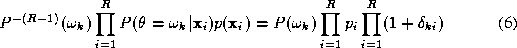
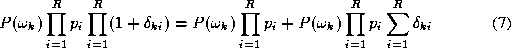
 we obtain a sum decision rule
we obtain a sum decision rule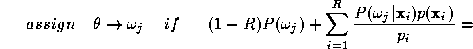
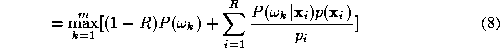
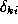 satisfies
satisfies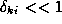 . It can be easily established that this condition will be satisfied if
. It can be easily established that this condition will be satisfied if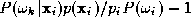 will be small in absolute value sense. Note that this condition will
hold when the amount of information about class identity of the object
gained by observing
will be small in absolute value sense. Note that this condition will
hold when the amount of information about class identity of the object
gained by observing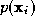 will be close to the reference value
will be close to the reference value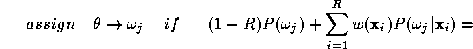
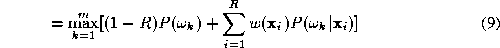
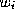 which will reflect the relative confidence in the experts in
expectation. This can be done easily by selecting weight values by means
of minimising the empirical classification error count produced by the
decision rule
which will reflect the relative confidence in the experts in
expectation. This can be done easily by selecting weight values by means
of minimising the empirical classification error count produced by the
decision rule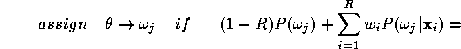
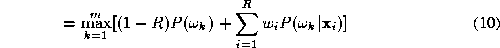
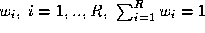 such that
such that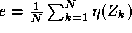 where
where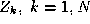 is the k-th training sample and
is the k-th training sample and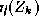 takes values
takes values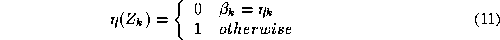
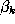 is the true class label of object
is the true class label of object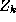 and
and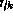 is the class label assigned to it by the decision rule (
is the class label assigned to it by the decision rule (