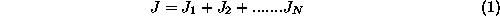
the set of surfaces and
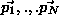the set of parameter vectors related to them. Each vector
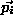has to minimize a given error criterion
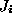associated with the surface
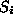. A reasonable criterion is the least squared error one. So let's
consider the following objective function composed of the sum of error
criterions
By considering the implicit equation representation of surfaces, a
surface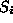
is represented by:
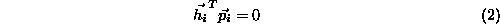
where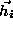
is the measurement vector. Note that any polynomially describable
surface can be presented in this scheme, as each component in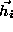
can be of the form
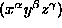for some
.
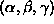Given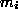
measurements, the least squares criterion related to this equation is
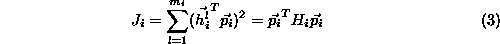
where {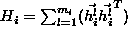
represents the sample covariance matrix of the surface
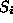. (We assume that the assignment of measurements to surfaces is known.)
The objective function (
1
) can then be written as :
By concatenating all the vectors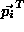
into one vector
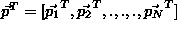equation (
4
) can be written as
Naoufel Werghi
