


Next:
Recovery of Surface Depth
Up:
Affine Reconstruction of Curved
Previous:
3D Motion and Image
We now consider how the camera motion can be computed from frontier
points,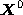 , on curved surfaces. Since a frontier point does not move before and
after the camera motion,
, on curved surfaces. Since a frontier point does not move before and
after the camera motion,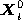 and
and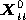 vanish. Substituting
vanish. Substituting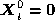 into (
3
), amd taking a vector product (
into (
3
), amd taking a vector product (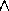 ) with
) with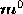 , we find that the magnitude of motion,
, we find that the magnitude of motion, , can be computed from the image measurements up to the depth to the
frontier point,
, can be computed from the image measurements up to the depth to the
frontier point,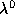 :
:
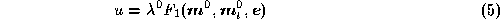
For the exact expression of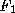 , see [
15
].
, see [
15
].
We next consider how the acceleration of the camera motion can be
computed from the frontier points. Substituting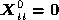 into (
4
), and taking a vector product with
into (
4
), and taking a vector product with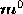 , the acceleration of the camera motion,
, the acceleration of the camera motion,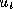 , can be computed from the image measurements as follows:
, can be computed from the image measurements as follows:
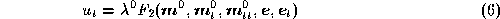
For the exact expression of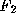 , see [
15
]. Note, even if the camera is uncalibrated, both
, see [
15
]. Note, even if the camera is uncalibrated, both and
and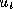 are computed from the changes in apparent contours in images up to the
depth
are computed from the changes in apparent contours in images up to the
depth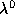 , and are independent of
, and are independent of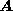 ,
,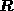 and
and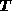 .
.
J. Sato
Mon Jul 7 22:39:50 BST 1997
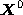 , on curved surfaces. Since a frontier point does not move before and
after the camera motion,
, on curved surfaces. Since a frontier point does not move before and
after the camera motion,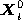 and
and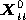 vanish. Substituting
vanish. Substituting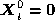 into (
3
), amd taking a vector product (
into (
3
), amd taking a vector product (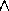 ) with
) with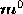 , we find that the magnitude of motion,
, we find that the magnitude of motion, , can be computed from the image measurements up to the depth to the
frontier point,
, can be computed from the image measurements up to the depth to the
frontier point,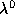 :
:


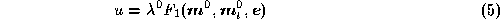
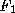 , see [
, see [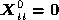 into (
into (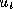 , can be computed from the image measurements as follows:
, can be computed from the image measurements as follows: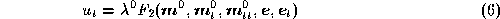
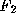 , see [
, see [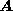 ,
,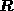 and
and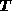 .
.