


Next:
4 Results
Up:
Progress in arbitrary topology
Previous:
2 Related work
The deformable surface that we use is based on the Generalised
Biquadratic B-Spline (GBBS) developed by Loop and De Rose [
10
,
11
] for computer graphics. It is a difficult task to compute the surface
due mainly to the difficulty of dealing with multi-indices of Bezier
simplices.
The GBBS is a powerful and elegant generalisation of the Biquadratic
B-Spline. It automatically maintains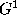 continuity. The GBBS is defined by a set of
M
3D control points
continuity. The GBBS is defined by a set of
M
3D control points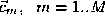 together with connectivity information. The connectivity defines a mesh
topology which is restricted to 4-sided faces, (see for example figure
1(b), 3(d)). Each vertex gives rise to an
n
-sided surface patch where
n
is the number of 4-sided faces using that vertex. Patch
m
depends only on the 2
n
+1 element control vector
together with connectivity information. The connectivity defines a mesh
topology which is restricted to 4-sided faces, (see for example figure
1(b), 3(d)). Each vertex gives rise to an
n
-sided surface patch where
n
is the number of 4-sided faces using that vertex. Patch
m
depends only on the 2
n
+1 element control vector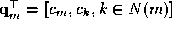 consisting of
consisting of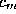 and the set of all vertices on adjacent faces, i.e. with
k
in the neighbourhood of
m
,
N
(
m
).
and the set of all vertices on adjacent faces, i.e. with
k
in the neighbourhood of
m
,
N
(
m
).
In this paper we introduce a new matrix-based scheme to compute the
surface based on notation similar to that of [
2
]. The principal steps in computing the surface are as follows. The
control vector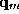 is converted to the Sabin net vector
is converted to the Sabin net vector by
by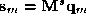 . The Sabin net vector is converted to a vector of Bezier control points
. The Sabin net vector is converted to a vector of Bezier control points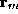 by another matrix
by another matrix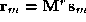 . This is combined with the Bezier polynomials
. This is combined with the Bezier polynomials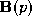 to compute the point. Thus we obtain the surface patch
to compute the point. Thus we obtain the surface patch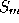 as a mapping from points
p
=(
u
,
v
) contained in a regular
n
-gon Domain
as a mapping from points
p
=(
u
,
v
) contained in a regular
n
-gon Domain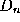 to a 3D surface
to a 3D surface
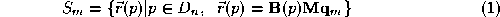
The whole surface
S
is the union of the patches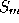 ,
,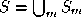 . The control vector for patch
m
,
. The control vector for patch
m
,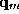 can be obtained from the vector of all control points
can be obtained from the vector of all control points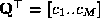 by a connectivity matrix
by a connectivity matrix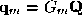 .
.
The remainder of this section is of a technical nature. We show how to
recast the generalised B-spline into the standard form used in computer
vision. Readers interested only in how to use the surface may skip to
the next section.
B-Splines are intimately related to Bezier curves [
14
,
5
]. When discussing Bezier curves it is useful to replace the usual
single parameter
u
with two parameters and
and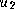 and a constraint that
and a constraint that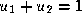 . A depth
d
Bezier curve
. A depth
d
Bezier curve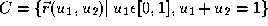 is defined in terms of
d
+1 control points
is defined in terms of
d
+1 control points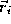 and the Bernstein-Bezier polynomials
and the Bernstein-Bezier polynomials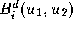 as follows
as follows
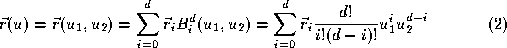
The Bezier curve admits an elegant generalisation called a B-form that
maps a [(
k
+1)-variate]
k
-dimensional parameter space onto any number of scalars. Firstly we must
define multivariate Bernstein-Bezier polynomials. For these we will need
a notation for multi-indices . The symbol
. The symbol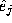 denotes a multi-index whose components are all zero except for the
j
component which is 1. It is useful to define a modulus of a multi-index
as
denotes a multi-index whose components are all zero except for the
j
component which is 1. It is useful to define a modulus of a multi-index
as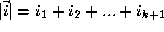 . The k-variate depth
d
Bernstein-Bezier polynomials are a simple generalisation of equation (
2
).
. The k-variate depth
d
Bernstein-Bezier polynomials are a simple generalisation of equation (
2
).
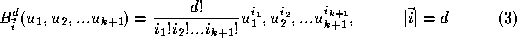
The Loop and De Rose scheme is based on S-patches, which are n-sided
smooth patches which map a point
p
=(
u
,
v
) inside
n
-sided domain polygon
D
to a 3D surface. Firstly we form
n
barycentric variables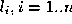 defined as follows. Define the
n
vertices of the regular
n
-gon as
defined as follows. Define the
n
vertices of the regular
n
-gon as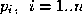 . Define the fractional areas
. Define the fractional areas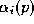 as the area of a triangle enclosed by points
p
,
as the area of a triangle enclosed by points
p
,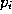 , and
, and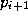 divided by the total area of
D
. Now form
n
new variables
divided by the total area of
D
. Now form
n
new variables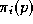 by
by
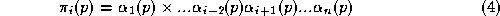
Then form normalised variables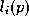
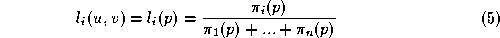
The S-patch is now simply defined in terms of the variables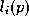 and the Bezier control points
and the Bezier control points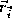 . It is a mapping
. It is a mapping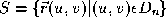 where
where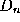 is a
n
-sided domain polygon and
is a
n
-sided domain polygon and
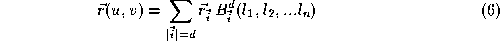
Note that the
n
-sided patch uses a
k
+1 variate Bezier polynomial where
n
=
k
+1. The fact that a different dimension multi-index is required for each
different sized patch is a bookkeeping headache for implementation.
The Bezier control points for a depth 5
n
-sided S-patch are computed from the Sabin net control points,
v
,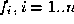 , and
, and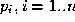 . Letting
. Letting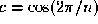 , then up to symmetries the Bezier control points are for
i
=1..
n
, then up to symmetries the Bezier control points are for
i
=1..
n
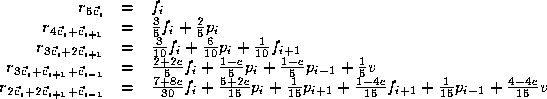
We now observe that this set of equations is a linear transform from the
Sabin net control points to the Bezier control points. Thus the
coefficients from the above equations may be used to populate the matrix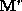 . (We note that some minor additional steps are necessary since this
leaves some matrix elements unspecified. Consult page 353 of [
11
] for details.) The Sabin net control points are obtained from the GBBS
control points by the recipe that
v
is the central vertex, the
. (We note that some minor additional steps are necessary since this
leaves some matrix elements unspecified. Consult page 353 of [
11
] for details.) The Sabin net control points are obtained from the GBBS
control points by the recipe that
v
is the central vertex, the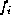 are centroids of each face, and the
are centroids of each face, and the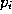 are centroids of each edge. This linear mapping can easily be converted
to the matrix
are centroids of each edge. This linear mapping can easily be converted
to the matrix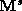 . If we rewrite equation
6
in matrix form as
. If we rewrite equation
6
in matrix form as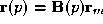 then we finally obtain
then we finally obtain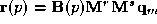 as required.
as required.
The constructive procedure specified above is lengthy and complex. We
firstly deal with the indexing problem. The multi-indices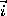 need to be converted to a one dimensional indexing scheme. Each index
may be interpreted as a number in base
d
+1, thus descending order in this value defines a unique mapping to a 1D
array. Enumeration of constant depth 1D array position to multi-index is
straightforwardly done through a lookup table, but the reverse lookup
table from multi-index to 1D array position is inconveniently large
since it is of size
need to be converted to a one dimensional indexing scheme. Each index
may be interpreted as a number in base
d
+1, thus descending order in this value defines a unique mapping to a 1D
array. Enumeration of constant depth 1D array position to multi-index is
straightforwardly done through a lookup table, but the reverse lookup
table from multi-index to 1D array position is inconveniently large
since it is of size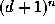 , (recall
d
=5,
n
= no. of sides). However the need for this table can be avoided.
, (recall
d
=5,
n
= no. of sides). However the need for this table can be avoided.
Next we must actually compute the sum specified in equation (
6
). Instead of the naive implementation we use the technique of de
Casteljau depth reduction [
5
]. This is a procedure by which a set of Bezier control points are
reduced iteratively in depth to
d
=0 which corresponds to a point. (This is in fact the basis for the
geometric interpretation of Bezier curves!) For the Bezier curve of
equation (
2
) we note that
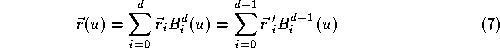
where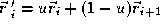 . This procedure generalises to a Bezier simplex. Thus we don't ever
need to compute the Bezier polynomials, we simply depth reduce the
control points recursively until
d
=0. The remaining trick to convenient computation is a lookup table with
the 1D array positions for depth reduction. In this way multi-indices
need never actually be used. This scheme is based on the suggestions of
Shoemake [
15
].
. This procedure generalises to a Bezier simplex. Thus we don't ever
need to compute the Bezier polynomials, we simply depth reduce the
control points recursively until
d
=0. The remaining trick to convenient computation is a lookup table with
the 1D array positions for depth reduction. In this way multi-indices
need never actually be used. This scheme is based on the suggestions of
Shoemake [
15
].
We have shown that we can compute points on the GBBS in the form . We now address the speed issues. There is no doubt that the
constructive procedure described above is between one and two orders of
magnitude slower than the equivalent tensor product B-Spline form. This
is partly because the number of Bezier control points (
. We now address the speed issues. There is no doubt that the
constructive procedure described above is between one and two orders of
magnitude slower than the equivalent tensor product B-Spline form. This
is partly because the number of Bezier control points (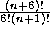 ) grows rapidly with
n
. The solution is to note that the vector
) grows rapidly with
n
. The solution is to note that the vector is only 2
n
+1 elements long and needs to be computed only once for each point
p
on the patch with fixed (
u
,
v
) coordinates.
is only 2
n
+1 elements long and needs to be computed only once for each point
p
on the patch with fixed (
u
,
v
) coordinates.
When it is necessary to render the patch we convert the patches by
subdivision into triangles and the same points
p
are always used. Thus lookup tables may be created in advance containing , and the computation for any point on the patch is reduced to 2
n
+1 multiply and add operations.
, and the computation for any point on the patch is reduced to 2
n
+1 multiply and add operations.
We minimise a cost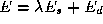 which balances a smoothness term
which balances a smoothness term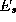 and a data force
and a data force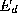 . The smoothness force may be written
. The smoothness force may be written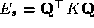 .
.
In our previous work the data force attached directly to the control
points rather than the surface itself. This is unsatisfactory. We now
show how to obtain a force which attaches directly to the surface
itself.
We suppose that the force arises from a volumetric potential energy term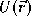 defined everywhere in space. All points on the surface should seek to
minimise this potential, i.e. we wish to minimise
defined everywhere in space. All points on the surface should seek to
minimise this potential, i.e. we wish to minimise
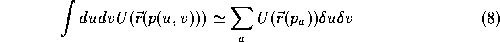
The integral is approximated as a discrete sum.
With the new matrix form of GBBS the data force becomes easier to
evaluate.
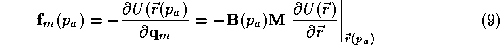
The total force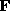 is made up of the sum over sample points
is made up of the sum over sample points and patches
m
.
and patches
m
.
The smoothness force that we use is very similar to that obtained by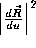 for curves. The force applied to each control point is equal to the
centroid of its edge neighbours less itself. A reaction force is applied
to the neighbours so that the overall force is always zero. Thus we
solve the dynamic equation
for curves. The force applied to each control point is equal to the
centroid of its edge neighbours less itself. A reaction force is applied
to the neighbours so that the overall force is always zero. Thus we
solve the dynamic equation

After convergence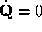 and a local minimum of
E
is achieved.
and a local minimum of
E
is achieved.



Next:
4 Results
Up:
Progress in arbitrary topology
Previous:
2 Related work
Andrew Stoddart
Thu Jul 10 17:16:18 BST 1997
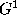 continuity. The GBBS is defined by a set of
M
3D control points
continuity. The GBBS is defined by a set of
M
3D control points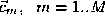 together with connectivity information. The connectivity defines a mesh
topology which is restricted to 4-sided faces, (see for example figure
1(b), 3(d)). Each vertex gives rise to an
n
-sided surface patch where
n
is the number of 4-sided faces using that vertex. Patch
m
depends only on the 2
n
+1 element control vector
together with connectivity information. The connectivity defines a mesh
topology which is restricted to 4-sided faces, (see for example figure
1(b), 3(d)). Each vertex gives rise to an
n
-sided surface patch where
n
is the number of 4-sided faces using that vertex. Patch
m
depends only on the 2
n
+1 element control vector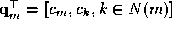 consisting of
consisting of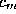 and the set of all vertices on adjacent faces, i.e. with
k
in the neighbourhood of
m
,
N
(
m
).
and the set of all vertices on adjacent faces, i.e. with
k
in the neighbourhood of
m
,
N
(
m
).


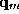 is converted to the Sabin net vector
is converted to the Sabin net vector by
by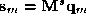 . The Sabin net vector is converted to a vector of Bezier control points
. The Sabin net vector is converted to a vector of Bezier control points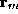 by another matrix
by another matrix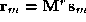 . This is combined with the Bezier polynomials
. This is combined with the Bezier polynomials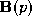 to compute the point. Thus we obtain the surface patch
to compute the point. Thus we obtain the surface patch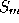 as a mapping from points
p
=(
u
,
v
) contained in a regular
n
-gon Domain
as a mapping from points
p
=(
u
,
v
) contained in a regular
n
-gon Domain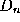 to a 3D surface
to a 3D surface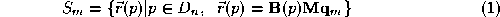
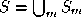 . The control vector for patch
m
,
. The control vector for patch
m
,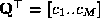 by a connectivity matrix
by a connectivity matrix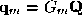 .
. and
and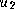 and a constraint that
and a constraint that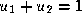 . A depth
d
Bezier curve
. A depth
d
Bezier curve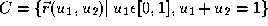 is defined in terms of
d
+1 control points
is defined in terms of
d
+1 control points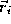 and the Bernstein-Bezier polynomials
and the Bernstein-Bezier polynomials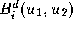 as follows
as follows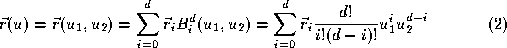
 . The symbol
. The symbol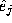 denotes a multi-index whose components are all zero except for the
j
component which is 1. It is useful to define a modulus of a multi-index
as
denotes a multi-index whose components are all zero except for the
j
component which is 1. It is useful to define a modulus of a multi-index
as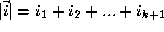 . The k-variate depth
d
Bernstein-Bezier polynomials are a simple generalisation of equation (
. The k-variate depth
d
Bernstein-Bezier polynomials are a simple generalisation of equation (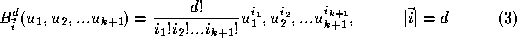
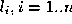 defined as follows. Define the
n
vertices of the regular
n
-gon as
defined as follows. Define the
n
vertices of the regular
n
-gon as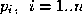 . Define the fractional areas
. Define the fractional areas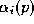 as the area of a triangle enclosed by points
p
,
as the area of a triangle enclosed by points
p
,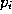 , and
, and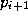 divided by the total area of
D
. Now form
n
new variables
divided by the total area of
D
. Now form
n
new variables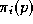 by
by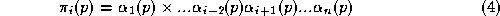
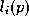
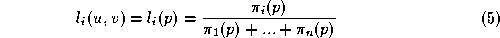
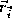 . It is a mapping
. It is a mapping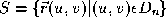 where
where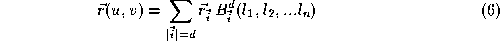
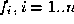 , and
, and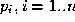 . Letting
. Letting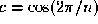 , then up to symmetries the Bezier control points are for
i
=1..
n
, then up to symmetries the Bezier control points are for
i
=1..
n
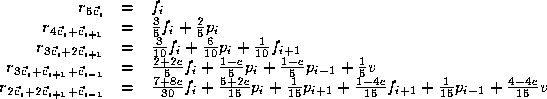
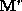 . (We note that some minor additional steps are necessary since this
leaves some matrix elements unspecified. Consult page 353 of [
. (We note that some minor additional steps are necessary since this
leaves some matrix elements unspecified. Consult page 353 of [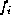 are centroids of each face, and the
are centroids of each face, and the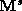 . If we rewrite equation
. If we rewrite equation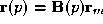 then we finally obtain
then we finally obtain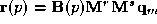 as required.
as required.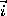 need to be converted to a one dimensional indexing scheme. Each index
may be interpreted as a number in base
d
+1, thus descending order in this value defines a unique mapping to a 1D
array. Enumeration of constant depth 1D array position to multi-index is
straightforwardly done through a lookup table, but the reverse lookup
table from multi-index to 1D array position is inconveniently large
since it is of size
need to be converted to a one dimensional indexing scheme. Each index
may be interpreted as a number in base
d
+1, thus descending order in this value defines a unique mapping to a 1D
array. Enumeration of constant depth 1D array position to multi-index is
straightforwardly done through a lookup table, but the reverse lookup
table from multi-index to 1D array position is inconveniently large
since it is of size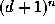 , (recall
d
=5,
n
= no. of sides). However the need for this table can be avoided.
, (recall
d
=5,
n
= no. of sides). However the need for this table can be avoided.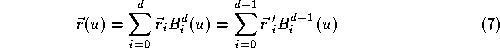
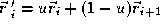 . This procedure generalises to a Bezier simplex. Thus we don't ever
need to compute the Bezier polynomials, we simply depth reduce the
control points recursively until
d
=0. The remaining trick to convenient computation is a lookup table with
the 1D array positions for depth reduction. In this way multi-indices
need never actually be used. This scheme is based on the suggestions of
Shoemake [
. This procedure generalises to a Bezier simplex. Thus we don't ever
need to compute the Bezier polynomials, we simply depth reduce the
control points recursively until
d
=0. The remaining trick to convenient computation is a lookup table with
the 1D array positions for depth reduction. In this way multi-indices
need never actually be used. This scheme is based on the suggestions of
Shoemake [ . We now address the speed issues. There is no doubt that the
constructive procedure described above is between one and two orders of
magnitude slower than the equivalent tensor product B-Spline form. This
is partly because the number of Bezier control points (
. We now address the speed issues. There is no doubt that the
constructive procedure described above is between one and two orders of
magnitude slower than the equivalent tensor product B-Spline form. This
is partly because the number of Bezier control points (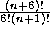 ) grows rapidly with
n
. The solution is to note that the vector
) grows rapidly with
n
. The solution is to note that the vector is only 2
n
+1 elements long and needs to be computed only once for each point
p
on the patch with fixed (
u
,
v
) coordinates.
is only 2
n
+1 elements long and needs to be computed only once for each point
p
on the patch with fixed (
u
,
v
) coordinates.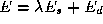 which balances a smoothness term
which balances a smoothness term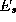 and a data force
and a data force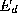 . The smoothness force may be written
. The smoothness force may be written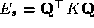 .
.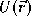 defined everywhere in space. All points on the surface should seek to
minimise this potential, i.e. we wish to minimise
defined everywhere in space. All points on the surface should seek to
minimise this potential, i.e. we wish to minimise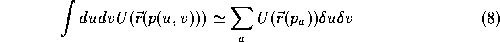
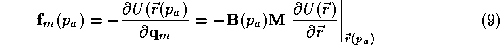
 is made up of the sum over sample points
is made up of the sum over sample points and patches
m
.
and patches
m
.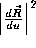 for curves. The force applied to each control point is equal to the
centroid of its edge neighbours less itself. A reaction force is applied
to the neighbours so that the overall force is always zero. Thus we
solve the dynamic equation
for curves. The force applied to each control point is equal to the
centroid of its edge neighbours less itself. A reaction force is applied
to the neighbours so that the overall force is always zero. Thus we
solve the dynamic equation
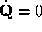 and a local minimum of
E
is achieved.
and a local minimum of
E
is achieved.