

Our approach is to assume that we do not know the exact form of the equation governing the observed color of objects in outdoor scenes. To recognize targets in outdoor scenes, we therefore need to select a classification scheme that performs well on arbitrarily shaped clusters in feature space. By definition, parametric classifiers (such as minimum-distance classifiers, as used by Crisman [ 5 ]) can be ruled out, since the underlying equations are unknown. Based on their success in other areas of non-parametric approximation, neural networks (i.e., feed-forward back-propagation nets) and multivariate decision trees were considered. Neural nets would presumably perform accurate nonlinear function approximation, but are difficult to analyze because of the arbitrary nature of the function approximated by the hidden layer. Multivariate decision trees create piecewise-linear approximations to surfaces in feature space by recursively dividing feature space with hyperplanes, and have been shown to produce good classification results from relatively few training samples.

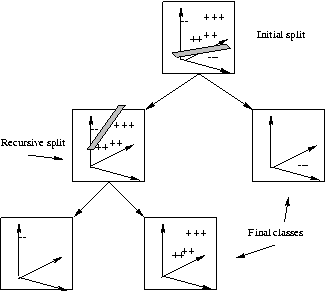
Figure 3:
Recursive discriminants of an MDT, separating the `+'s from the `-'s
(top), and MDT structure with LTU's and final classes (bottom).
Multivariate decision trees [ 2 ] recursively subdivide the feature space by linear threshold units (LTU's). Each LTU is a binary test represented by linear combinations of feature values and associated weights. Each division attempts to separate, in a set of known instances (the training set), target instances from non-targets. If the two resulting subsets are linearly separable, a single LTU will separate them and the multivariate decision tree consists of the single node. If not (as is generally the case with realistic images and objects), the LTU linearly divides the feature space so as to separate the instances to the extent possible, and the MDT creates and trains new LTU's on the two divisions of the instances. The result, therefore, is a tree of LTU's recursively dividing the feature space into polygons so as to perform a piecewise linear approximation of the region in color-space consisting of the positive samples. The terminal nodes in the tree correspond to inseparable sets, which are labeled as individual classes. Thus, each node in a decision tree is either a decision or a class. Figure 3 (left) shows a decision-tree operating in a three-dimensional feature space, where the two classes being separated are the '+'s and the '-'s; Brodley [ 2 ] describes further details.
The LTU weights are approximated using the Recursive Least Squares (RLS) algorithm, which minimizes the mean squared error between the estimated (y_I) and true (y_i) values, (Summation((y_i - y_I)^2)) of the selected features over a number of training instances. RLS incrementally updates the weight vector W according to W_k = W_(k-1) - K_k * (transpose(X_k) * W_(k-1) - y_k), where W_k is the weight vector for the instance k, of size n, W_(k-1) is the weight vector for instance (k-1), X_k is the instance vector; (transpose(X_k)) is X_k transposed, and y_k is the class of the instance. K_k = P_k * X_k, where P_k is the (n x n) covariance matrix for instance k, reflecting the uncertainty in the weights, and P_k = P_(k-1) - P_(k-1) * (X_k [1 + transpose(X_k) * P_(k-1) * X_k]^(-1)) * (transpose(X_k)) * (P_(k-1)). The weights are initialized randomly, and the matrix consists of 0 values everywhere except along the diagonal, which is set to 10^6 (empirically determined).
If at any level, the LTU results in a non-negative value, the corresponding set of pixels is labeled as belonging to the object (i.e., positive), otherwise, it is labeled negative. If the set of instances at any level can be further divided, the tree is recursively grown; if no further division is possible, that set of instances is represented by a terminal node or a class (with the LTU determining whether the class is positive or negative). Figure 3 (right) shows the structure of a multivariate decision tree. In this tree, the non-terminal nodes represent the LTU tests, and the leaf nodes the classes; the `+' leaf nodes correspond to the inseparable sets classified as one class, and the `-' nodes, the other.
Like other non-parametric learning techniques, decision trees are susceptible to over-training. In order to correct for over-fitting, a fully grown tree can pruned by determining the classification error for each non-leaf subtree, and then comparing it to the classification error resulting from replacing the subtree with a leaf-node bearing the class label of the majority of the training instances in the set. If the leaf-node results in better performance, the subtree is replaced by it [ 2 ].


Shashi Buluswar