4 Improving feature detection

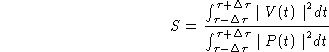
In this section we turn our attention to improving the measurement process. We consider two ways in which this can be done; replacing the visual edge feature detector by an acoustic boundary feature enhancement operator; and using spatio-temporal based speckle noise reduction prior to boundary detection.

The visual image tracking algorithm uses a gradient-based operator for detecting contour points which produces many candidate responses on ultrasound images. This is due partly to the low signal-to-noise ratio and poor image contrast. There is, however, something fundamentally wrong with using such an approach. A gradient-based feature detector is designed to detect an object boundary as a step discontinuity in intensity. However, an ideal acoustic edge is defined as a discontinuity in acoustic impedance (an intensity ridge) or equivalently a discontinuity in acoustic energy or integrated backscatter (IBS). Formerly, integrated backscatter is defined as,

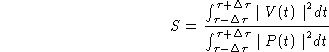
where S indicates the integrated backscatter measure, V ( t ) and P ( t ) are the signals received from the tissue and the reflector, respectively, is the position in time of the centre of the region of interest in the tissue and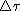 is the corresponding half-width in time. In the spatial domain, integrated backscatter can be estimated simply as the average squared greylevels over a neighbourhood. The IBS model has been used to measure properties of myocardial tissue since changes in integrated backscatter relate to changes in acoustic impedance, and hence changes in tissue relaxation and elasticity [ 8 ]. IBS boundary enhancement is also used in state-of-the-art commercial echocardiographic imaging systems for single view real-time edge detection.

We investigated tracking heart boundaries on image sequences pre-filtered by an IBS algorithm to see if this improved tracking performance. IBS filtering removed a significant amount of speckle noise within the left ventricle chamber and enhanced heart chamber boundaries but the result was blurred relative to the original. Overall there were less spurious feature responses but localisation of heart contours did not improve due to spatial blurring.

A natural question to ask is whether spatio-temporal filtering can improve ultrasound feature detection relative to a static image feature detection approach. Herlin and Ayache explored this idea for step edge detection in ultrasound images [ 6 ]. They assumed a step model and Gaussian noise.

We implemented a spatio-temporal acoustic boundary detection scheme based on a combination of spatio-temporal speckle reduction filtering [ 4 ] and acoustic energy discontinuity detection. Figure 4 shows one frame together with IBS enhanced and spatio-temporal speckle-reduced/IBS enhanced versions of the same images. A frame-by-frame visual comparison of tracking using the three approaches showed that the reliability of detection of boundaries was best for the spatio-temporal boundary detection algorithm. Quantifying the degree of improvement is difficult because we do not have any ground truth by which to compare the algorithms. However, since we can estimate the state vectors we can look for consistency of state vector component trajectories over a number of cycles as a measure of algorithm robustness to measurement noise. In figure 5 we show coefficient plots based on tracking on the original data (light curve) and the data pre-filtered by the spatio-temporal boundary enhancement method (dark curve). Observe that the plots are more consistent for the algorithm which used the spatio-temporal filtering approach.

The current approach involving the sequential application of a temporal-based noise-reduction filter followed by static image feature detection gives improved tracking performance. However, further improvement could be achieved if temporal information was utilised in the detection step. We are currently exploring methods to extend the idea of spatio-temporal acoustic boundary detection to a truly 3D (2D+T) filtering process.

   
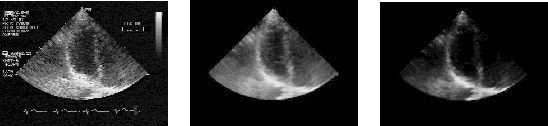
Figure 4: Noise reduction. The original ultrasound image (left), the image after the two-dimensional least mean square (TDLMS) filter is applied (middle), TDLMS filter followed by IBS (right).

   
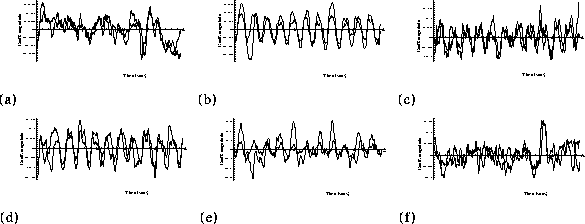
Figure 5: Comparison of component plots for tracking on ultrasound data -- original data (light curve) and enhanced data (dark line) using an affine matrix. Each component is plotted against the time for the image sequence.