


Next:
3 The rectification transformation
Up:
Rectification with unconstrained stereo
Previous:
1 Introduction and motivations
Following [
4
], we consider a stereo pair composed of two pinhole cameras, each
modelled by its
optical center
 and its
retinal plane
(or
image plane
)
and its
retinal plane
(or
image plane
)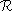 . In each camera, a point
. In each camera, a point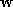 in 3-D space is projected into an image point
in 3-D space is projected into an image point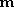 , which is the intersection of the line
, which is the intersection of the line with
with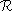 . The transformation from
. The transformation from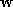 to
to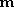 is modelled by the linear transformation
is modelled by the linear transformation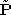 in projective (or homogeneous) coordinate:
in projective (or homogeneous) coordinate:

where
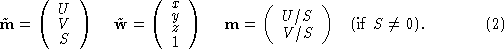
The points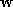 for which
S
=0 define the
focal plane
and are projected to infinity. The projection matrix
for which
S
=0 define the
focal plane
and are projected to infinity. The projection matrix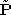 can be decomposed into the product
can be decomposed into the product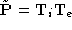 .
.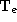 maps from world to camera coordinates and depends on the extrinsic
parameters of the stereo rig only;
maps from world to camera coordinates and depends on the extrinsic
parameters of the stereo rig only;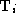 , which maps from camera to pixel coordinates and depends on the
intrinsic parameters only, has the following form:
, which maps from camera to pixel coordinates and depends on the
intrinsic parameters only, has the following form:
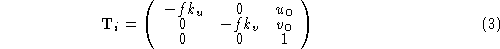
where
f
is the focal length in millimeters,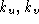 are the scale factors along the
u
and
v
axes respectively (the number of pixels per millimiter), and
are the scale factors along the
u
and
v
axes respectively (the number of pixels per millimiter), and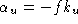 , and
, and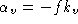 are the focal lengths in horizontal and vertical pixels, respectively.
If we write the projection matrix as
are the focal lengths in horizontal and vertical pixels, respectively.
If we write the projection matrix as
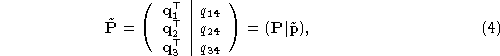
we see that the plane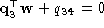 (
S
=0) is the focal plane, and the two planes
(
S
=0) is the focal plane, and the two planes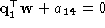 and
and intersect the retinal plane in the vertical (
U
=0) and horizontal (
V
=0) axis of the retinal coordinates, respectively.
intersect the retinal plane in the vertical (
U
=0) and horizontal (
V
=0) axis of the retinal coordinates, respectively.
The
optical center
, , is the intersection of the three planes introduced in the previous
paragraph; therefore
, is the intersection of the three planes introduced in the previous
paragraph; therefore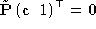 , and
, and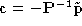 . The
optical ray
associated to an image point
. The
optical ray
associated to an image point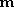 is the line
is the line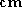 , i.e. the set of points
, i.e. the set of points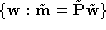 . The equation of this ray can be written in parametric form as
. The equation of this ray can be written in parametric form as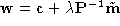 .
.



Next:
3 The rectification transformation
Up:
Rectification with unconstrained stereo
Previous:
1 Introduction and motivations
Adrian F Clark
Wed Jul 23 16:48:44 BST 1997
 and its
retinal plane
(or
image plane
)
and its
retinal plane
(or
image plane
) . In each camera, a point
. In each camera, a point in 3-D space is projected into an image point
in 3-D space is projected into an image point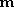 , which is the intersection of the line
, which is the intersection of the line with
with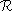 . The transformation from
. The transformation from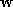 to
to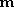 is modelled by the linear transformation
is modelled by the linear transformation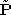 in projective (or homogeneous) coordinate:
in projective (or homogeneous) coordinate:



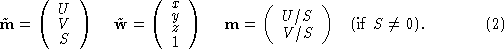
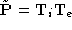 .
.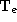 maps from world to camera coordinates and depends on the extrinsic
parameters of the stereo rig only;
maps from world to camera coordinates and depends on the extrinsic
parameters of the stereo rig only;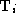 , which maps from camera to pixel coordinates and depends on the
intrinsic parameters only, has the following form:
, which maps from camera to pixel coordinates and depends on the
intrinsic parameters only, has the following form: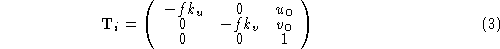
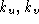 are the scale factors along the
u
and
v
axes respectively (the number of pixels per millimiter), and
are the scale factors along the
u
and
v
axes respectively (the number of pixels per millimiter), and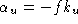 , and
, and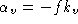 are the focal lengths in horizontal and vertical pixels, respectively.
If we write the projection matrix as
are the focal lengths in horizontal and vertical pixels, respectively.
If we write the projection matrix as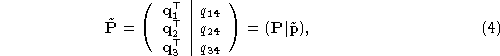
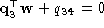 (
S
=0) is the focal plane, and the two planes
(
S
=0) is the focal plane, and the two planes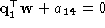 and
and intersect the retinal plane in the vertical (
U
=0) and horizontal (
V
=0) axis of the retinal coordinates, respectively.
intersect the retinal plane in the vertical (
U
=0) and horizontal (
V
=0) axis of the retinal coordinates, respectively.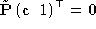 , and
, and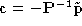 . The
optical ray
associated to an image point
. The
optical ray
associated to an image point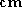 , i.e. the set of points
, i.e. the set of points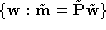 . The equation of this ray can be written in parametric form as
. The equation of this ray can be written in parametric form as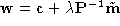 .
.