Next: Visual Traffic Understanding Up: Vehicle Tracking with Applications Previous: Introduction

Motion Estimation

The motion estimation consists of two stages. Firstly, the camera motion is determined using point matches. Secondly, localisation of potential vehicles is determined using optical flow.

Egomotion

The robust and reliable determination of the camera motion (or egomotion) is a well studied problem. For a comparative analysis of different methods for estimating egomotion the reader is referred to [ 14 ]. However, such approaches fail to provide reliable estimates for road scenes. A novel 3-D approach is presented in the next section, followed by a qualitative discussion in relation to the shortcomings of other approaches.

3-D Approach

A new approach has been developed which uses a calibrated camera (see Section: Experimental Results ) and features in the ground plane close to the camera. The complete algorithm is shown in Figure 3 .

For each frame in the sequence the image is warped to yield a plan view of the ground plane (see Figure 4(a)) . This requires knowledge of the current camera position and the internal calibration to be known and constant. The warping is based on a bi-linear interpolation. The Harris-Stephens corner detector is applied to the warped image to extract salient point features, typically line endpoints. The detection of features is more reliable in this ``ground-plane'' image than the original image as the effects of perspective projection have been removed. These features give a set of points in real world coordinates on the ground. The real world points can then be projected into the warped image for the next frame given an assumed camera motion. The normalised correlations between the local neighbourhoods of these points gives a score which is used to refine the camera motion parameters (translation ( X , Y ), Pan, Tilt) using the simplex search algorithm [ 10 ]. The underlying assumption of the method is that the features tracked are on the ground-plane. The key advantage of this technique is that reliable egomotion estimates can be obtained on a frame-to-frame basis. Figure 4(b) shows the recovered egomotion parameters (2nd row: forward translation Y, 3rd row: sideways translation X, top row: normalised correlation score) for a typical motorway sequence of 250 frames. The results are consistent with expectations ( footnote ) except for one frame (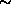 150). Despite this one gross error tracking continued successfully due to the smoothing action of the Kalman filter. Note that the graphs show measured (not filtered) data.

Comparison with other approaches

The approach described above is efficient in that the correlation of the ground-plane image and the next image is only performed in the neighbourhood of previously detected features. A commonly used alternative approach is based on the image-plane detection matching of corners and/or lines. Experiments were performed on the computation of the focus of expansion using the renormalisation approach of [ 7 ] combined with a robust RANSAC estimator [ 4 ]. This approach constrains the motion to be purely translational. However, reliable egomotion estimates (up to a speed-scale ambiguity) have only been obtained when the image contains significant image structure (e.g. motorway bridges). Furthermore, estimation using consecutive frames is unreliable because background feature points typically have small disparities. Ideally, egomotion estimates should be computed on a frame-to-frame basis. However, neither of the two egomotion approaches discussed (renormalisation or 3-D method) provide reliable estimates on images such as Figure 1(a). In such scenes, model-based tracking of the white lines and region-based matching methods are more appropriate for egomotion estimation.

Independent Motion

A number of optical flow techniques were investigated for their ability to detect independent motion. In this work, the optical flow for a given frame of an image sequence is computed using the differential technique of [ 9 ] within a Gaussian pyramidal framework. The highest resolution is 256 by 256 pixels. The image sequence is prefiltered with spatial ( = 1.0) Gaussian smoothing. The image velocities are computed from the spatiotemporal derivatives of the image intensities. In this case, a second-order method employs a global smoothness constraint term in an iterative relaxation scheme to compute dense optical flow over the whole image. To localise vehicles the optical flow vectors are clustered into regions based on proximity. The method assumes that vehicles are not overlapping significantly. Ideally, background motion estimates could be used to drive the segmentation process. However, experiments have shown that camera vibration significantly affects flow estimates. It is unclear as to whether (1) the camera motion parameters contributing to the vibration (e.g. Pan, Tilt) can be recovered accurately enough to stabilse the images, and (2) if the background motion can be recovered with sufficient accuracy to drive the segmentation process. Although the technique used here can generate false positives it is sufficient to bootstrap the model-based techniques described in the next part of the paper.

Next: Visual Traffic Understanding Up: Vehicle Tracking with Applications Previous: Introduction