


Next:
4 On-the-fly training
Up:
Adaptive Segmentation of Ultrasound
Previous:
2 B-spline and piecewise
We turn now to the particular problem of ultrasound image segmentation.
Compared with other medical imaging modalities (eg. CT and MRI)
ultrasound is particularly difficult to segment since the quality of the
images is relatively low. In particular, organ boundaries are not always
prominent -- see Figure
2
. Fully automatic techniques for ultrasound image segmentation are not
likely to be robust. Instead we make sensible use of operator
assistance, through snakes, to produce fast and reliable segmentations
with the minimal amount of manual intervention.
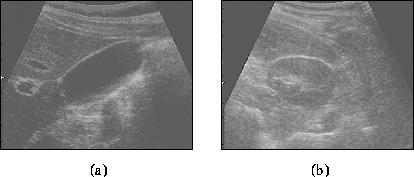
Figure 2:
Organ boundaries in ultrasound images.
The gall blagger (a) is a fluid filled cavity which is fairly difficult
to segment. Note how the boundary is not characterised by a high
gradient everywhere: the boundary properties are not stationary. The
kidney (b) is even more challenging to segment since tissue-tissue
boundaries are relatively difficult to localise in ultrasound images.
To guide the snakes, we need to define potential functions based on
image properties. In addition to the intensity gradient, which will be
of limited use, it is reasonable to attempt some sort of texture
segmentation [
9
,
13
], though the noise properties of the ultrasound images suggest that
looking at anything beyond second order grey level statistics is
pointless. We therefore attempt segmentation based on two properties:
-
1D intensity gradients along the B-spline snake's search lines
-
First and second order grey level statistics
Both properties are measured after smoothing with a Gaussian kernel of
standard deviation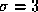 pixels. This reduces the speckle but preserves meaningful image
structure.
pixels. This reduces the speckle but preserves meaningful image
structure.
The texture segmentation is performed as follows. Given an initial
segmentation, we gather texture statistics from both sides of the
boundary and derive an optimal discriminator between inside and outside
(or equivalently, for open splines, left and right) -- see Figure
3
. We represent the texture statistics of a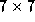 patch centered on (
x
,
y
) as the vector
patch centered on (
x
,
y
) as the vector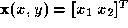 , where
, where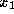 is the mean of the intensities in the patch and
is the mean of the intensities in the patch and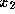 is their variance. We then calculate the mean
is their variance. We then calculate the mean of the
x
's sampled from the ``inside'' class
of the
x
's sampled from the ``inside'' class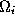 , and also their covariance matrix
, and also their covariance matrix . Likewise, we calculate the corresponding quantities
. Likewise, we calculate the corresponding quantities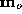 and
and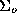 for samples taken from the ``outside'' class
for samples taken from the ``outside'' class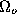 . Assuming the class-conditional density functions
. Assuming the class-conditional density functions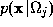 are independent normal distributions, the optimal discriminator is [
2
]:
are independent normal distributions, the optimal discriminator is [
2
]:
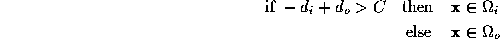
where
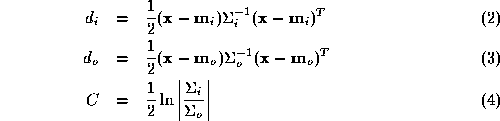
Since the texture statistics are generally not stationary around the
boundary, we compute ,
,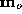 ,
, and
and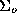 locally for each of the spline segments
locally for each of the spline segments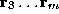 .
.
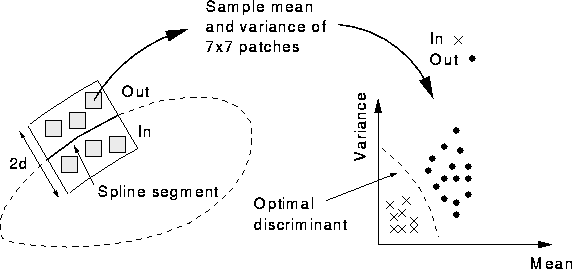
Figure 3:
Texture classification.
A texture classifier is trained for each spline segment by sampling the
mean and variance of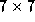 patches within the search window and finding the optimal discriminant
between ``in'' and ``out'' patches.
patches within the search window and finding the optimal discriminant
between ``in'' and ``out'' patches.
We can now define potential functions for both intensity and
texture-based segmentation. The potential functions are calculated along
each of the B-spline snake's search lines and local minima provide the
target points :
:
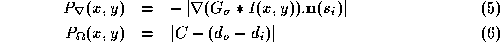
where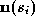 is a unit vector along the search line. It is not immediately apparent
which potential function will perform best, and indeed this will vary
for different images, or even at different portions of the boundary in a
single image. We therefore propose to use a linear combination of the
two, with on-the-fly training to adaptively select the appropriate
weights.
is a unit vector along the search line. It is not immediately apparent
which potential function will perform best, and indeed this will vary
for different images, or even at different portions of the boundary in a
single image. We therefore propose to use a linear combination of the
two, with on-the-fly training to adaptively select the appropriate
weights.



Next:
4 On-the-fly training
Up:
Adaptive Segmentation of Ultrasound
Previous:
2 B-spline and piecewise
A.H. Gee
Wed Jun 25 12:11:11 BST 1997




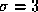 pixels. This reduces the speckle but preserves meaningful image
structure.
pixels. This reduces the speckle but preserves meaningful image
structure.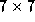 patch centered on (
x
,
y
) as the vector
patch centered on (
x
,
y
) as the vector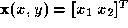 , where
, where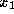 is the mean of the intensities in the patch and
is the mean of the intensities in the patch and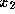 is their variance. We then calculate the mean
is their variance. We then calculate the mean of the
x
's sampled from the ``inside'' class
of the
x
's sampled from the ``inside'' class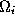 , and also their covariance matrix
, and also their covariance matrix . Likewise, we calculate the corresponding quantities
. Likewise, we calculate the corresponding quantities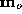 and
and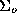 for samples taken from the ``outside'' class
for samples taken from the ``outside'' class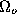 . Assuming the class-conditional density functions
. Assuming the class-conditional density functions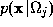 are independent normal distributions, the optimal discriminator is [
are independent normal distributions, the optimal discriminator is [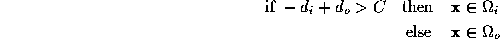
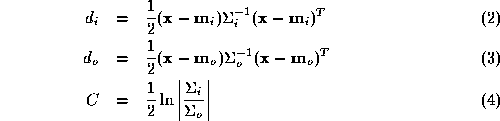
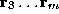 .
.
 :
: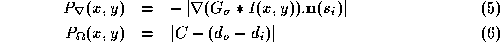
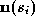 is a unit vector along the search line. It is not immediately apparent
which potential function will perform best, and indeed this will vary
for different images, or even at different portions of the boundary in a
single image. We therefore propose to use a linear combination of the
two, with on-the-fly training to adaptively select the appropriate
weights.
is a unit vector along the search line. It is not immediately apparent
which potential function will perform best, and indeed this will vary
for different images, or even at different portions of the boundary in a
single image. We therefore propose to use a linear combination of the
two, with on-the-fly training to adaptively select the appropriate
weights.