For the purpose of defining an adaptative filter, Yang et al [
3
] proposed a technique for defining and computing a measure of
anisotropism at each point within an image. In that paper, the issue of
corner identification has been addressed. Here we show how it can be
extended to corner orientation detection.
For a strongly orientated intensity pattern along one direction, the
power spectrum clusters along a line through the origin in the Fourier
domain. By determining this line, and how closely it approximates the
Fourier transform of the image, the orientation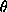
and the strength
g
of the anisotropism of the pattern can be derived. It has been
demonstrated that the computation of
g
and
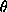does not require the actual computation of the Fourier transform.
Indeed, the analytical expressions obtained are:
with the same notations as those used in Equation (
1
). In Equations (
2
) and (
3
)
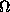is a small neighbourhood of
. This scheme uses single derivatives only, which are integrated, and
thus it reduces the effect of noise.
The value of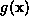
is 1 for a strongly orientated pattern along one direction, and is 0 for
isotropic regions. For real images with a low signal-to-noise ratio,
this method proves to be more robust than the mere estimation of the
gradient direction.
In order to apply the above technique to corner recognition, we introduce two assumptions about the characteristic features of corners:
with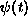
being a monotonic decreasing function from 1 to 0 within [0:1]. In our
implementation, we chose:
with
m
=2 typically. Figure 1
1
shows an example of the computation of the fields required for
estimating cornerness. (a) is the original synthetic image. (b) shows
the gradient magnitude. (c) shows the anisotropism which is high along
the edges and low at corner points. (d) and (e) show cornerness with
different window settings. The orientation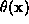
which is required at a later stage of the algorithm, is also given,
shown as (f).
Figure 1:
a) Original image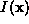
. b) Gradient magnitude
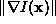. c) Anisotropism
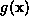. Straight edges are strongly anisotropic along one direction whereas
corner points are not. d) Cornerness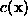
. e) Cornerness
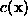with different window settings: precise corner pixels can be identified.
f) Direction of anisotropism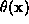
(on a gray-scale from 0 - black to
- white). It gives the orientation of the edges, but cannot be used
within the immediate neighbourhood of corners.
Extracting the actual corner points is achieved by analysing the
histogram of the cornerness image. A small proportion of pixels (
) with sufficiently high values can be regarded as belonging to corners.
Each cluster of such points is labelled as one corner, at the position
of its point of highest cornerness. Experiments show that some simple
edge points may be misclassified as corners this way, especially if
is chosen too high and for noisy images. This, however, has little
detrimental effect on the algorithm, since at a later stage these pixels
can be easily identified and discarded.
F. Chabat
