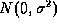 . In this case, analysing the difference in intensity images is
straightforward. Differencing followed by taking the absolute value will
produce the Normal distribution
. In this case, analysing the difference in intensity images is
straightforward. Differencing followed by taking the absolute value will
produce the Normal distribution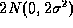 for positive values only.
for positive values only.


In many instances it is reasonable to assume that the image noise can be
modelled by a zero mean Normal distribution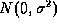 . In this case, analysing the difference in intensity images is
straightforward. Differencing followed by taking the absolute value will
produce the Normal distribution
. In this case, analysing the difference in intensity images is
straightforward. Differencing followed by taking the absolute value will
produce the Normal distribution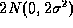 for positive values only.
for positive values only.
Sometimes it is preferred to difference edge maps rather than intensity images as they can be more robust for change detection under varying illumination [ 1 , 21 , 25 ]. Unfortunately this makes determining the distribution of the noise more troublesome. First we note that the noise in the edge maps can be modelled by a Rayleigh distribution [ 24 ]

if the edge response is of the form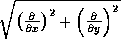 . Denoting the noise in two edge maps as independent random variables
a
and
b
we wish to calculate the density of the noise in the difference image
. Denoting the noise in two edge maps as independent random variables
a
and
b
we wish to calculate the density of the noise in the difference image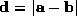 . Initially we consider the symmetric function
. Initially we consider the symmetric function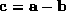 . Its density
. Its density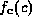 equals the convolution of the densities of
equals the convolution of the densities of and
and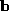 [
14
]
[
14
]
For the Rayleigh functions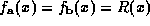 we obtain, using Mathematica,
we obtain, using Mathematica,
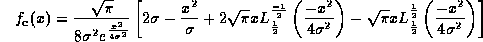
where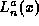 is the generalised Laguerre polynomial. Since
is the generalised Laguerre polynomial. Since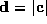 , then
, then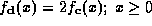 (this assumes that
(this assumes that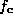 is even, although it is actually undefined for negative values in the
form given above).
is even, although it is actually undefined for negative values in the
form given above).
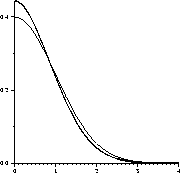
Figure 1:
Probability density function of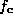 and
N
(0,1)
and
N
(0,1)
Looking at the plot of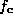 drawn bold alongside a Normal distribution (figure
1
) we see that they are similar, especially near the tails. We are mainly
interested in the distribution function towards the tails since we wish
to threshold out most of the noise. Therefore we can reasonably
approximate
drawn bold alongside a Normal distribution (figure
1
) we see that they are similar, especially near the tails. We are mainly
interested in the distribution function towards the tails since we wish
to threshold out most of the noise. Therefore we can reasonably
approximate by a Normal distribution. When thresholding at
by a Normal distribution. When thresholding at the probability of incorrectly classifying a pixel as motion is
the probability of incorrectly classifying a pixel as motion is

This enables us to choose a suitable threshold for a given acceptable proportion of false motion pixels.
for a given acceptable proportion of false motion pixels.
In practise the variance of the noise is often unknown so we need to estimate it from the image. Since the difference image will contain not just noise but also appreciable amounts of signal due to the motion a robust estimation technique is required. Similar to our previous work in estimating noise levels in edge maps [ 16 ] we use the Least Median of Squares (LMedS) method applied to the difference image histogram. Its advantages are that it is efficient (at least for 1D data), and has a high breakdown point. This latter property enables it to return the correct result even when large amounts of outliers (i.e. true motion) are present. It is straightforward [ 17 ] to derive the following relation between the LMedS and the expected standard deviation of the noise:




Paul L Rosin