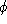 over the curve
G
that approximates the contour.
over the curve
G
that approximates the contour.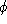 could be, for example, the distance of the contour from the center of
mass of the image as a function of arc-length as in Figure (1).
could be, for example, the distance of the contour from the center of
mass of the image as a function of arc-length as in Figure (1).


Size functions [
3
,
4
] are topological descriptions of generic 2D shapes. They are invariant
with respect to translation and scale and they are robust with respect
to small variations of shape. In this work, they are used, as in [
9
], to characterize the occluding contour of the hand. To compute a size
function, one must first define a continous real-valued measuring
function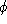 over the curve
G
that approximates the contour.
over the curve
G
that approximates the contour.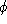 could be, for example, the distance of the contour from the center of
mass of the image as a function of arc-length as in Figure (1).
could be, for example, the distance of the contour from the center of
mass of the image as a function of arc-length as in Figure (1).

|
|
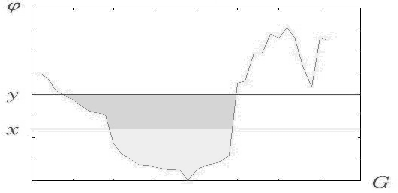
Figure 1:
(Left) The occluding contour
G
of the hand. (Right) A continuous measuring function on
G
, in this case
G
is partitioned by
x
and
y
in one equivalence class.
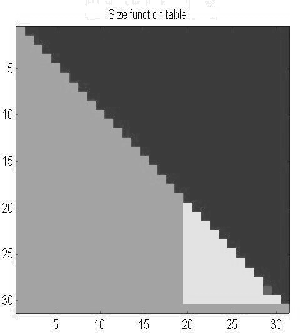
The size function is determined by computing, for every pair of values
x
and
y
in the range of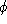 , the number of connected components of the subgraph
, the number of connected components of the subgraph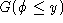 which contain at least an element of
which contain at least an element of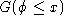 . This consists in calculating the number of equivalence classes in
which
. This consists in calculating the number of equivalence classes in
which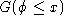 is partitioned by the relationship
is partitioned by the relationship defined below [
9
]:
defined below [
9
]:
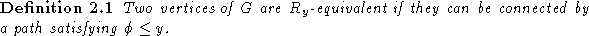
The integer-valued function of the pair (
x
,
y
) obtained in this fashion is called size function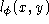 . It can be easily shown that all the information is contained in the
triangular region
. It can be easily shown that all the information is contained in the
triangular region
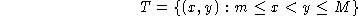
where
m
and
M
are the minimum and maximum values of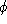 over
G
.
over
G
.
|
 .
.
To fully represent the shape of the contour, one needs a family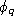 of measuring functions. Since the meaning of signs does not depend on
the position and distance of the hand with respect to the camera, the
measuring functions should be invariant for translation over the image
plane and scale.
of measuring functions. Since the meaning of signs does not depend on
the position and distance of the hand with respect to the camera, the
measuring functions should be invariant for translation over the image
plane and scale.
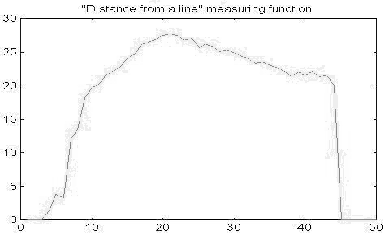
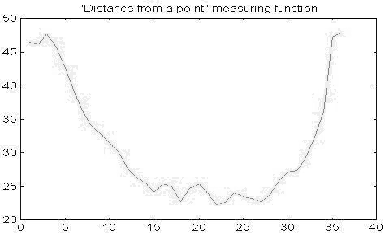
We used, as in [ 9 ], two different families, called respectively distance from a line segment and distance from a point. The definitions are explained in Figures (3) and (4) respectively.
The representation consists in a collection of size functions, one for
each measuring function in the two defined families. It is a cumbersome
representation, however, experimental results seem to prove that, due to
its redundancy, a size function can be characterized by its mean value.
Each size function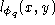 is piecewise constant and monotonic along
x
and
y
separately, hence, the entire information resides in the location and
value of the jumps of
is piecewise constant and monotonic along
x
and
y
separately, hence, the entire information resides in the location and
value of the jumps of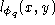 along
x
and
y
which correspond only to few integer numbers.
along
x
and
y
which correspond only to few integer numbers.

|
|

|
|



Adrian F Clark