


Next:
4 Merging Shapes
Up:
A Method of
Previous:
2 Background
This section describes a correspondence algorithm which produces a
mapping between two triangulated surfaces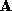 and
and . In our case, the 3D surface is defined as a set of planar contours.
Each contour represents the outline of a 3D object as it appears in a
single 2D slice of a 3D image. The vertices of these contours are the
pointsets
. In our case, the 3D surface is defined as a set of planar contours.
Each contour represents the outline of a 3D object as it appears in a
single 2D slice of a 3D image. The vertices of these contours are the
pointsets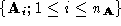 and
and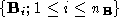 . The connectivity of each pointset is generated from its contour
representation using the algorithm of Geiger [
5
]. This produces densely triangulated polyhedral surface
representations. We assume that the geometric information of each
surface has been normalised such that the centre-of-gravity is at the
origin and the mean distance of the points from the origin is 1. The
output of the algorithm is a pair of sparse polyhedrons
. The connectivity of each pointset is generated from its contour
representation using the algorithm of Geiger [
5
]. This produces densely triangulated polyhedral surface
representations. We assume that the geometric information of each
surface has been normalised such that the centre-of-gravity is at the
origin and the mean distance of the points from the origin is 1. The
output of the algorithm is a pair of sparse polyhedrons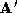 and
and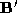 for which
for which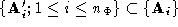 and
and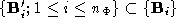 . Pairs of labelled vertices from these polyhedrons comprise a set of
. Pairs of labelled vertices from these polyhedrons comprise a set of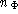 correspondences. The connectivity of each of the corresponding polyhedra
is identical. The pair-wise correspondence algorithm comprises two
stages:
correspondences. The connectivity of each of the corresponding polyhedra
is identical. The pair-wise correspondence algorithm comprises two
stages:
-
Generation of sparse polyhedral approximations of the input shapes
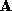 and
and ,
,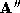 and
and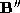 by triangle decimation; for which
by triangle decimation; for which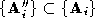 and
and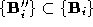 . The connectivity descriptions of vertices in these polyhedra are
updated during the decimation process. This reduces the computational
complexity of the correspondence task. No correspondences are
established between the pair of shapes at this stage, and the
polyhedrons will usually have a different number of vertices i.e.
. The connectivity descriptions of vertices in these polyhedra are
updated during the decimation process. This reduces the computational
complexity of the correspondence task. No correspondences are
established between the pair of shapes at this stage, and the
polyhedrons will usually have a different number of vertices i.e.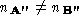 .
. -
Generation of a corresponding pair of sparse polygons
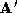 and
and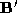 . This is accomplished using a global Euclidean measure of similarity
between both the sparse polyhedron
. This is accomplished using a global Euclidean measure of similarity
between both the sparse polyhedron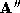 and a subset of labelled vertices from
and a subset of labelled vertices from and between
and between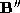 and a subset from
and a subset from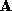 . The connectivity and number of vertices from either
. The connectivity and number of vertices from either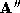 or
or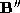 is chosen to define the polyhedra
is chosen to define the polyhedra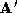 and
and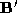 from the labelled vertices
from the labelled vertices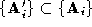 and
and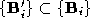 .
.
These two steps will now be described in greater detail.
To generate a sparse polyhedron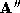 representing
representing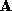 , we have used a modified version of the triangle mesh decimation
algorithm of Schroeder
et al
[
10
]. The original decimation algorithm had three stages:
, we have used a modified version of the triangle mesh decimation
algorithm of Schroeder
et al
[
10
]. The original decimation algorithm had three stages:
-
Each vertex of the triangle mesh of is characterised by local geometry
and topology and labelled with one of five classifications, this step
requires the definition of a threshold
feature angle
.
-
A decimation criterion is evaluated for each vertex
 based upon a distance metric
based upon a distance metric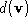 appropriate to its classification. If
appropriate to its classification. If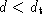 where
where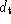 is some target distance, then the vertex is removed.
is some target distance, then the vertex is removed. -
The hole left by removing a vertex is filled by re-triangulation.
The algorithm is implemented by making multiple passes over all vertices
in the mesh until some termination criterion is met. This criterion may
be based on either the number of vertices left in the mesh or upon
d
.
Our adaptation of this algorithm makes use of a
volume
metric rather than a distance metric for the decimation criterion. This
is analogous to the
area
metric of the Critical Point Detection (CPD) [
15
] algorithm used for the decimation of polygons in the 2D version of
this landmarking framework. The use of a volume metric allows us to
treat all of the vertices of a mesh uniformly and to dispense with the
vertex characterisation step of the algorithm. As a consequence of this,
we may also dispense with the definition of a threshold feature angle.
The volume metric is computed using Schroeder's distance to mean plane
measure. The mean plane associated with a vertex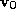 is defined by a unit normal
is defined by a unit normal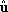 and weighted centroid
and weighted centroid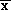 which are defined using the
which are defined using the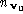 triangles connected to
triangles connected to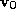 :
:
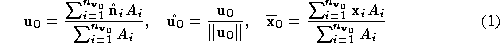
where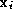 ,
,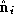 and
and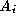 are respectively the centroids, unit surface normals and areas of
triangle
are respectively the centroids, unit surface normals and areas of
triangle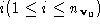 connected to
connected to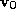 . The volume metric is computed as:
. The volume metric is computed as:
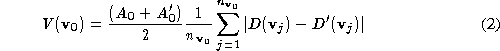
where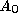 and
and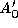 are the sums of the areas of the triangles in the loop before and after
decimation respectively, and
are the sums of the areas of the triangles in the loop before and after
decimation respectively, and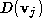 and
and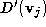 are the
signed
distances of the vertex
are the
signed
distances of the vertex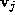 to the mean plane of the loop before and after decimation i.e.
to the mean plane of the loop before and after decimation i.e.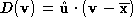 . By decimation it is meant that the vertex associated with the loop has
been removed and the resulting hole re-triangulated. Re-triangulation of
the hole is by a recursive loop-splitting algorithm which seeks to fill
the hole with triangles of high aspect ratio.
. By decimation it is meant that the vertex associated with the loop has
been removed and the resulting hole re-triangulated. Re-triangulation of
the hole is by a recursive loop-splitting algorithm which seeks to fill
the hole with triangles of high aspect ratio.
The decimation algorithm is implemented by keeping a list of vertices sorted by increasing
sorted by increasing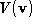 . The head of this list is iteratively decimated and the list updated
until a target number of vertices for the sparse polyhedron is met.
Again, this is analogous to the CPD algorithm used for polygon
decimation. Thus, a sparse polyhedral approximation to our original
triangulated mesh is produced which consists of a subset of vertices of
that mesh, see Figure 1.
. The head of this list is iteratively decimated and the list updated
until a target number of vertices for the sparse polyhedron is met.
Again, this is analogous to the CPD algorithm used for polygon
decimation. Thus, a sparse polyhedral approximation to our original
triangulated mesh is produced which consists of a subset of vertices of
that mesh, see Figure 1.

Figure 1:
Result of applying the decimation algorithm to a triangulated surface of
the left ventricle of the brain. On the left is a shaded representation
of the original dense triangulation with approximately 2000 vertices. On
the right the same surface decimated by 90%.
This stage of the algorithm introduces the only control parameter in the
algorithm - the target number of vertices that should be left in the
sparse polyhedral representation after decimation. We have determined
empirically that the removal of 90% of the original vertices gives an
adequate shape representation whilst decreasing the computational cost
of finding correspondences and merging shapes in the subsequent stages
of the algorithm.
We have used the Iterative Closest Point (ICP) algorithm described by
Besl and McKay [
2
] to establish correspondences between the vertices of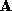 and
and . The ICP algorithm determines the Euclidean transformation required to
map one pointset onto another pointset without any initial
correspondence information. We have used a
symmetric
version of this algorithm to establish correspondences of the sparse
pointset
. The ICP algorithm determines the Euclidean transformation required to
map one pointset onto another pointset without any initial
correspondence information. We have used a
symmetric
version of this algorithm to establish correspondences of the sparse
pointset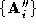 with the dense pointset
with the dense pointset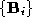 and of the sparse pointset
and of the sparse pointset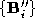 with the dense pointset
with the dense pointset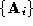 . Producing correspondences using the sparse polyhedra which have been
generated by decimation cuts down the computational cost of this stage
of the algorithm. The symmetric ICP algorithm is as follows:
. Producing correspondences using the sparse polyhedra which have been
generated by decimation cuts down the computational cost of this stage
of the algorithm. The symmetric ICP algorithm is as follows:

The pointsets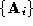 and
and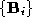 are the vertices of the original densely triangulated surfaces, the
subsets
are the vertices of the original densely triangulated surfaces, the
subsets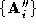 and
and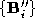 are the vertices of the decimated surfaces. An initial estimate of the
pose
Q
is made by finding the translation required to register the centroids of
the pointsets in an intermediate frame, and the scaling required to
equalise the average chord length (average distance from all points to
centroid) of the two pointsets.
are the vertices of the decimated surfaces. An initial estimate of the
pose
Q
is made by finding the translation required to register the centroids of
the pointsets in an intermediate frame, and the scaling required to
equalise the average chord length (average distance from all points to
centroid) of the two pointsets.
Various metrics can be used to define the
best
match between pointsets. We have used a symmetric measurement of the
distance error in registration of the pointsets. We minimise this error
such that the pose
Q
which satisfies:
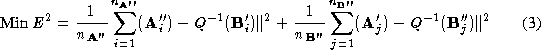
is determined, where
Q
represents the Euclidean transformation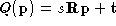 , s is a scale factor,
, s is a scale factor,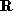 is a rotation matrix and
is a rotation matrix and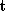 is a translation. This measures the point registration errors in an
intermediate frame rather than in either frame
is a translation. This measures the point registration errors in an
intermediate frame rather than in either frame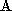 or frame
or frame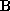 .
.
The connectivity of the polyhedra may be used to improve the performance
of the algorithm by using information about the surface normals at each
point. We weight the squared distance between points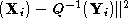 by a factor of
by a factor of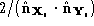 where
where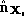 is the unit surface normal on
is the unit surface normal on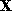 at point
i
, to encourage the correspondence of points on the surfaces which are
topologically equivalent.
at point
i
, to encourage the correspondence of points on the surfaces which are
topologically equivalent.
A single corresponding pair of sparse polyhedra must now be established
from the two polyhedron/pointset pairs,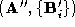 and
and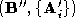 . The choice of connectivity is not critical and so we choose the
connectivity of
. The choice of connectivity is not critical and so we choose the
connectivity of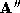 (the binary tree framework causes the error of the match to be tested
for both pair orderings). This choice defines one of the corresponding
sparse polyhedra
(the binary tree framework causes the error of the match to be tested
for both pair orderings). This choice defines one of the corresponding
sparse polyhedra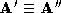 . The connectivity description of
. The connectivity description of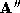 is now combined with the pointset
is now combined with the pointset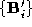 to produce a pair of matching polyhedra with a one-to-one mapping
to produce a pair of matching polyhedra with a one-to-one mapping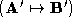 . The number of correspondences
. The number of correspondences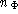 has now been determined:
has now been determined: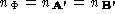 .
.



Next:
4 Merging Shapes
Up:
A Method of
Previous:
2 Background
Alan Brett
Wed Jul 9 16:24:02 BST 1997
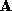 and
and . In our case, the 3D surface is defined as a set of planar contours.
Each contour represents the outline of a 3D object as it appears in a
single 2D slice of a 3D image. The vertices of these contours are the
pointsets
. In our case, the 3D surface is defined as a set of planar contours.
Each contour represents the outline of a 3D object as it appears in a
single 2D slice of a 3D image. The vertices of these contours are the
pointsets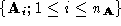 and
and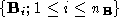 . The connectivity of each pointset is generated from its contour
representation using the algorithm of Geiger [
5
]. This produces densely triangulated polyhedral surface
representations. We assume that the geometric information of each
surface has been normalised such that the centre-of-gravity is at the
origin and the mean distance of the points from the origin is 1. The
output of the algorithm is a pair of sparse polyhedrons
. The connectivity of each pointset is generated from its contour
representation using the algorithm of Geiger [
5
]. This produces densely triangulated polyhedral surface
representations. We assume that the geometric information of each
surface has been normalised such that the centre-of-gravity is at the
origin and the mean distance of the points from the origin is 1. The
output of the algorithm is a pair of sparse polyhedrons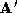 and
and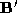 for which
for which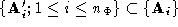 and
and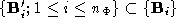 . Pairs of labelled vertices from these polyhedrons comprise a set of
. Pairs of labelled vertices from these polyhedrons comprise a set of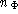 correspondences. The connectivity of each of the corresponding polyhedra
is identical. The pair-wise correspondence algorithm comprises two
stages:
correspondences. The connectivity of each of the corresponding polyhedra
is identical. The pair-wise correspondence algorithm comprises two
stages:


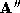 and
and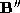 by triangle decimation; for which
by triangle decimation; for which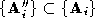 and
and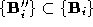 . The connectivity descriptions of vertices in these polyhedra are
updated during the decimation process. This reduces the computational
complexity of the correspondence task. No correspondences are
established between the pair of shapes at this stage, and the
polyhedrons will usually have a different number of vertices i.e.
. The connectivity descriptions of vertices in these polyhedra are
updated during the decimation process. This reduces the computational
complexity of the correspondence task. No correspondences are
established between the pair of shapes at this stage, and the
polyhedrons will usually have a different number of vertices i.e.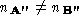 .
.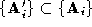 and
and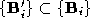 .
. based upon a distance metric
based upon a distance metric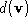 appropriate to its classification. If
appropriate to its classification. If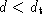 where
where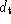 is some target distance, then the vertex is removed.
is some target distance, then the vertex is removed.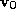 is defined by a unit normal
is defined by a unit normal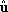 and weighted centroid
and weighted centroid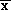 which are defined using the
which are defined using the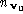 triangles connected to
triangles connected to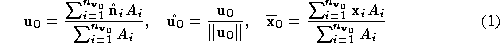
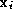 ,
,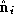 and
and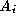 are respectively the centroids, unit surface normals and areas of
triangle
are respectively the centroids, unit surface normals and areas of
triangle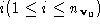 connected to
connected to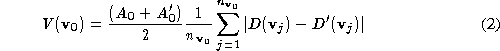
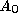 and
and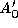 are the sums of the areas of the triangles in the loop before and after
decimation respectively, and
are the sums of the areas of the triangles in the loop before and after
decimation respectively, and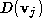 and
and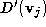 are the
signed
distances of the vertex
are the
signed
distances of the vertex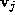 to the mean plane of the loop before and after decimation i.e.
to the mean plane of the loop before and after decimation i.e.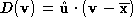 . By decimation it is meant that the vertex associated with the loop has
been removed and the resulting hole re-triangulated. Re-triangulation of
the hole is by a recursive loop-splitting algorithm which seeks to fill
the hole with triangles of high aspect ratio.
. By decimation it is meant that the vertex associated with the loop has
been removed and the resulting hole re-triangulated. Re-triangulation of
the hole is by a recursive loop-splitting algorithm which seeks to fill
the hole with triangles of high aspect ratio.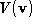 . The head of this list is iteratively decimated and the list updated
until a target number of vertices for the sparse polyhedron is met.
Again, this is analogous to the CPD algorithm used for polygon
decimation. Thus, a sparse polyhedral approximation to our original
triangulated mesh is produced which consists of a subset of vertices of
that mesh, see Figure 1.
. The head of this list is iteratively decimated and the list updated
until a target number of vertices for the sparse polyhedron is met.
Again, this is analogous to the CPD algorithm used for polygon
decimation. Thus, a sparse polyhedral approximation to our original
triangulated mesh is produced which consists of a subset of vertices of
that mesh, see Figure 1.
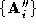 with the dense pointset
with the dense pointset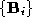 and of the sparse pointset
and of the sparse pointset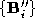 with the dense pointset
with the dense pointset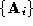 . Producing correspondences using the sparse polyhedra which have been
generated by decimation cuts down the computational cost of this stage
of the algorithm. The symmetric ICP algorithm is as follows:
. Producing correspondences using the sparse polyhedra which have been
generated by decimation cuts down the computational cost of this stage
of the algorithm. The symmetric ICP algorithm is as follows:
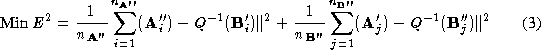
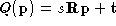 , s is a scale factor,
, s is a scale factor, is a rotation matrix and
is a rotation matrix and is a translation. This measures the point registration errors in an
intermediate frame rather than in either frame
is a translation. This measures the point registration errors in an
intermediate frame rather than in either frame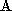 or frame
or frame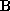 .
.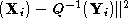 by a factor of
by a factor of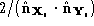 where
where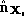 is the unit surface normal on
is the unit surface normal on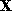 at point
i
, to encourage the correspondence of points on the surfaces which are
topologically equivalent.
at point
i
, to encourage the correspondence of points on the surfaces which are
topologically equivalent.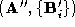 and
and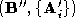 . The choice of connectivity is not critical and so we choose the
connectivity of
. The choice of connectivity is not critical and so we choose the
connectivity of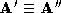 . The connectivity description of
. The connectivity description of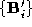 to produce a pair of matching polyhedra with a one-to-one mapping
to produce a pair of matching polyhedra with a one-to-one mapping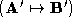 . The number of correspondences
. The number of correspondences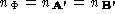 .
.