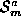 and
and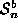 , provides 3 constraints on the 6 parameter rigid transformation,
, provides 3 constraints on the 6 parameter rigid transformation,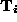 , where:
, where:



The alignment of a pair of planar patches,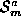 and
and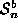 , provides 3 constraints on the 6 parameter rigid transformation,
, provides 3 constraints on the 6 parameter rigid transformation,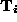 , where:
, where:
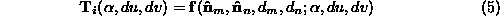
In homogeneous coordinates this can be expressed as the product of a
rotation,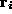 , and a translation,
, and a translation,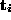 .
.
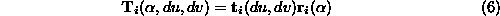
The rotation constraint is the set of rotations that align the surface
patch normals,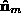 with
with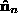 . This is determined by finding an arbitrary rotation that aligns
. This is determined by finding an arbitrary rotation that aligns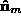 with
with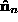 and then rotating around
and then rotating around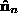 . We can align
. We can align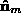 with
with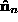 by rotating by
by rotating by radians about the bisector,
radians about the bisector,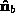 , to
, to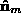 and
and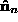 . This gives the value of the constraint at
. This gives the value of the constraint at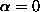 .
.
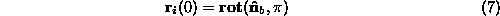
where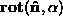 describes the rotation around an axis defined by
describes the rotation around an axis defined by by
by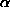 radians. A good reference for this can be found in [
11
]. The constraint is then found by rotating around
radians. A good reference for this can be found in [
11
]. The constraint is then found by rotating around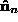 .
.
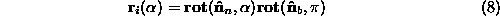
The translation that aligns a pair of planes is only constrained in the direction of the plane normals. Note that the first plane has now been rotated so that it is parallel with the second.
We now define a pair of orthogonal vectors and
and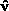 , which are mutually orthogonal to the plane normals
, which are mutually orthogonal to the plane normals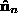 , such that:
, such that:
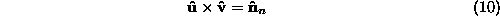
The translation constraint is then given by:
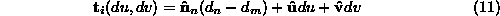



Anthony Ashbrook