


Next:
3 Experiments
Up:
Segmentation of Range Data
Previous:
1 Introduction
Given a pair of range images of an articulated object,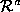 and
and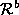 , the goal is to segment the range data into subimages where each
subimage represents a rigid subset of the data. We present an overview
of our proposed segmentation algorithm here, followed by a more detailed
description the most important stages.
, the goal is to segment the range data into subimages where each
subimage represents a rigid subset of the data. We present an overview
of our proposed segmentation algorithm here, followed by a more detailed
description the most important stages.
-
Segment the range data into surface patches
Each of the range images,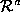 and
and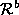 , is segmented into a set of surface patches,
, is segmented into a set of surface patches,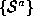 and
and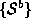 respectively. Currently, only planar patches are used by later stages of
the algorithm.
respectively. Currently, only planar patches are used by later stages of
the algorithm.
-
For each surface patch in
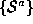 find corresponding patches in
find corresponding patches in
Geometric constraints may be used to form correspondences between
surfaces patches. In the work presented here, however, we consider each
planar patch in to be a potential correspondence with each planar patch in
to be a potential correspondence with each planar patch in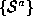 .
.
-
Determine constraints on the rigid transformations that align object
subcomponents from surface patch correspondences
Each correct surface patch correspondence provides a constraint on the
rigid transformation that aligns the object subcomponent that the
surfaces belong to. Incorrect surface correspondences will provide
erroneous constraints but these will be rejected later.
-
Vote for each rigid transformation constraint in a discretized parameter
space
A Hough transform is used to accumulate evidence for the transformations
that align each of the object subcomponents. Surface patches belonging
to the same subcomponent will provide constraints which intersect at the
correct alignment transformation parameters, producing a peak in the
Hough space. The 6-parameter rigid, transformation space is partitioned
into a 3-parameter rotation space and a 3-parameter translations space
for efficiency.
-
The largest peak in the parameter space is found and surface patches
which contributed to the peak are noted as belonging to the same rigid
subcomponent and then removed
The rigid transformation which accounts for most of the data in the
range images is identified by finding the largest peak in the Hough
space. If the constraint provided by a pair of corresponding surfaces
passes close to the peak then those surfaces are removed. The removed
surfaces provide the required segmentation.
-
Steps 4 and 5 are repeated until no more peaks can be found
The Hough transform is reconstructed using the remaining surfaces to
find the next most significant subcomponent. This is repeated until no
more peaks are found in the Hough transform.
We have used a surface patch segmentation algorithm which segments the
surface data into quadric patches using the local surface curvature. The
full details of this algorithm can be found in the literature [
8
,
9
,
10
] but can be summarised as follows:
-
The range data is smoothed using edge preserving, diffusion smoothing.
-
The mean and Gaussian curvatures are calculated at each data point.
-
Seed surface patches are formed by grouping neighbouring pixels whose
mean and Gaussian curvature have the same sign.
-
Seed patches are either eliminated or cleaned up using a morphological
operator.
-
Quadric surfaces are fitted to the seed patches and pixels are regrouped
according to the surface patch they are closest to. This is repeated
until a stable segmentation is obtained.
In the future we intend to use generic quadric patches to segment range
data into rigid subsets but we currently only use planar patches.
Each pair of corresponding surface patches provides a constraint,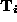 , on the parameters of a rigid transformation. For planar surface
patches the constraint fixes 3 of the 6 degrees of freedom and can be
defined as:
, on the parameters of a rigid transformation. For planar surface
patches the constraint fixes 3 of the 6 degrees of freedom and can be
defined as:
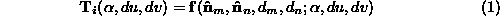
where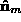 and
and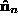 are the surface normals of the two patches and
are the surface normals of the two patches and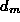 and
and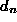 are the corresponding perpendicular distances from the surfaces to the
origin. The details of the function
are the corresponding perpendicular distances from the surfaces to the
origin. The details of the function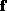 are presented in Appendix A. The parameters
are presented in Appendix A. The parameters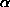 ,
du
and
dv
represent the remaining degrees of freedom.
,
du
and
dv
represent the remaining degrees of freedom.
In the absence of measurement error, each of the constraints on the
transformation of a particular subcomponent will intersect at the
appropriate point in the parameter space. In practice, measurement
errors are inevitable and unless these are accounted for in an
appropriate manner, the robustness of the segmentation algorithm will
suffer.
To ensure robust performance, measurement errors are propagated through
the algorithm to determine the error on each of the constraints. If the
errors on all of the plane parameters are represented by the covariance
matrix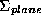 (these errors are themselves calculated by error propagation) then the
error on each constraint
(these errors are themselves calculated by error propagation) then the
error on each constraint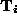 can be approximated as:
can be approximated as:
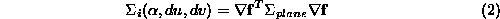
where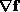 is the matrix of partial derivatives of
is the matrix of partial derivatives of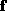 with respect to the plane parameters, commonly known as the Jacobian
matrix.
with respect to the plane parameters, commonly known as the Jacobian
matrix.
Having established the error on each constraint we can establish a
probability density function,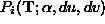 , to integrate into the Hough transform instead of making a single vote.
In fact, it is the logarithm of
, to integrate into the Hough transform instead of making a single vote.
In fact, it is the logarithm of which is integrated into the Hough transform so as to turn a product of
probabilities into a sum of independent terms. For convenience we make
the simplifying assumption that the errors are Gaussian so that:
which is integrated into the Hough transform so as to turn a product of
probabilities into a sum of independent terms. For convenience we make
the simplifying assumption that the errors are Gaussian so that:
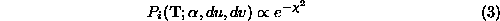
where:
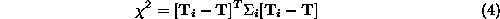
This provides a probability for each cell in the Hough space, defined by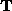 , which is a function of the parameters
, which is a function of the parameters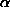 ,
du
and
dv
. To evaluate this probability we choose parameter values which maximise
,
du
and
dv
. To evaluate this probability we choose parameter values which maximise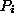 . The result is that each constraint is now
smeared
in the parameter space according to its sensitivity to measurement
errors. It is worth noting the relationship between the constraint error
and the size of the planar patches used to derive the constraint. For
small patches the error on each of the plane parameters is relatively
large which results in a more
smeared
constraint entry in the Hough transform. For large patches the
constraint entry becomes much sharper as the constraint error is small.
. The result is that each constraint is now
smeared
in the parameter space according to its sensitivity to measurement
errors. It is worth noting the relationship between the constraint error
and the size of the planar patches used to derive the constraint. For
small patches the error on each of the plane parameters is relatively
large which results in a more
smeared
constraint entry in the Hough transform. For large patches the
constraint entry becomes much sharper as the constraint error is small.



Next:
3 Experiments
Up:
Segmentation of Range Data
Previous:
1 Introduction
Anthony Ashbrook
Fri Jul 11 10:33:28 BST 1997
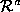 and
and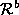 , the goal is to segment the range data into subimages where each
subimage represents a rigid subset of the data. We present an overview
of our proposed segmentation algorithm here, followed by a more detailed
description the most important stages.
, the goal is to segment the range data into subimages where each
subimage represents a rigid subset of the data. We present an overview
of our proposed segmentation algorithm here, followed by a more detailed
description the most important stages.


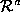 and
and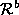 , is segmented into a set of surface patches,
, is segmented into a set of surface patches,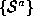 and
and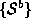 respectively. Currently, only planar patches are used by later stages of
the algorithm.
respectively. Currently, only planar patches are used by later stages of
the algorithm.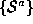 find corresponding patches in
find corresponding patches in
 to be a potential correspondence with each planar patch in
to be a potential correspondence with each planar patch in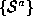 .
.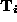 , on the parameters of a rigid transformation. For planar surface
patches the constraint fixes 3 of the 6 degrees of freedom and can be
defined as:
, on the parameters of a rigid transformation. For planar surface
patches the constraint fixes 3 of the 6 degrees of freedom and can be
defined as: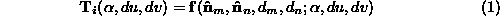
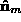 and
and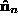 are the surface normals of the two patches and
are the surface normals of the two patches and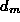 and
and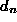 are the corresponding perpendicular distances from the surfaces to the
origin. The details of the function
are the corresponding perpendicular distances from the surfaces to the
origin. The details of the function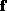 are presented in Appendix A. The parameters
are presented in Appendix A. The parameters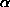 ,
du
and
dv
represent the remaining degrees of freedom.
,
du
and
dv
represent the remaining degrees of freedom.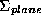 (these errors are themselves calculated by error propagation) then the
error on each constraint
(these errors are themselves calculated by error propagation) then the
error on each constraint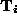 can be approximated as:
can be approximated as: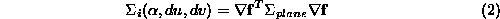
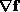 is the matrix of partial derivatives of
is the matrix of partial derivatives of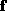 with respect to the plane parameters, commonly known as the Jacobian
matrix.
with respect to the plane parameters, commonly known as the Jacobian
matrix.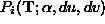 , to integrate into the Hough transform instead of making a single vote.
In fact, it is the logarithm of
, to integrate into the Hough transform instead of making a single vote.
In fact, it is the logarithm of which is integrated into the Hough transform so as to turn a product of
probabilities into a sum of independent terms. For convenience we make
the simplifying assumption that the errors are Gaussian so that:
which is integrated into the Hough transform so as to turn a product of
probabilities into a sum of independent terms. For convenience we make
the simplifying assumption that the errors are Gaussian so that: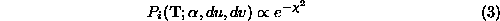
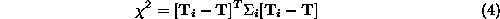
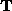 , which is a function of the parameters
, which is a function of the parameters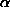 ,
du
and
dv
. To evaluate this probability we choose parameter values which maximise
,
du
and
dv
. To evaluate this probability we choose parameter values which maximise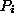 . The result is that each constraint is now
smeared
in the parameter space according to its sensitivity to measurement
errors. It is worth noting the relationship between the constraint error
and the size of the planar patches used to derive the constraint. For
small patches the error on each of the plane parameters is relatively
large which results in a more
smeared
constraint entry in the Hough transform. For large patches the
constraint entry becomes much sharper as the constraint error is small.
. The result is that each constraint is now
smeared
in the parameter space according to its sensitivity to measurement
errors. It is worth noting the relationship between the constraint error
and the size of the planar patches used to derive the constraint. For
small patches the error on each of the plane parameters is relatively
large which results in a more
smeared
constraint entry in the Hough transform. For large patches the
constraint entry becomes much sharper as the constraint error is small.