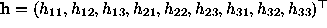 the homogeneous equations (
1
) for
n
points become
the homogeneous equations (
1
) for
n
points become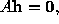 with
A
the
with
A
the matrix:
matrix: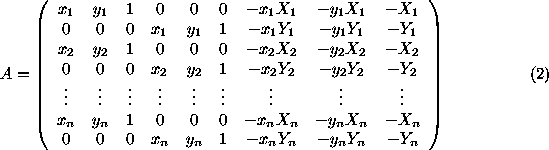


From equation ( 1 ) each image to world point correspondence provides two equations linear in the H matrix elements. For n correspondences we obtain a system of 2 n equation in 8 unknowns. If n = 4 then an exact solution is obtained. Otherwise, if n > 4, the matrix is over determined, and H is estimated by a suitable minimisation scheme.
The covariance of the estimated H matrix depends both on the errors in the position of the points used for its computation and the estimation method. There are three standard methods for estimating H :
Writing the
H
matrix in vector form as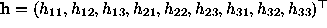 the homogeneous equations (
1
) for
n
points become
the homogeneous equations (
1
) for
n
points become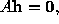 with
A
the
with
A
the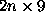 matrix:
matrix:
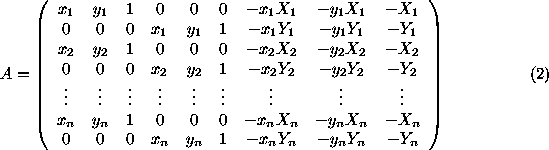
It is a standard result of linear algebra that the vector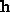 that minimises the algebraic residuals
that minimises the algebraic residuals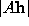 , subject to
, subject to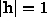 , is given by the eigenvector of least eigenvalue of
, is given by the eigenvector of least eigenvalue of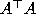 . This eigenvector can be obtained directly from the SVD of
A
. In the case of
n
= 4,
. This eigenvector can be obtained directly from the SVD of
A
. In the case of
n
= 4, is the null-vector of
A
and the residuals are zero.
is the null-vector of
A
and the residuals are zero.


Antonio Criminisi