


Next:
6 Modelling the spatial
Up:
Thresholding for Change Detection
Previous:
4 Modelling the signal
If we assume that the noise is white then its spatial distribution over
the image will be random. For the analysis of spatial data there are
many measures of randomness [
23
], often based on the assumption that the observations follow a Poisson
distribution. Since a Poisson distribution has its mean equal to its
variance then the ratio of the sample variance to the sample mean is a
natural test for that distribution, and is called the
relative variance
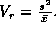 It is calculated by first counting the number of observations (in our
case the number of above threshold pixels in the difference map) in
n
windows,
It is calculated by first counting the number of observations (in our
case the number of above threshold pixels in the difference map) in
n
windows,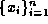 , from which the mean,
, from which the mean,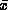 , and variance,
, and variance,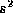 , of the
, of the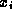 can be found. Although the test is sensitive to the window size and
point density it works adequately as long as
can be found. Although the test is sensitive to the window size and
point density it works adequately as long as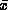 is sufficiently large.
is sufficiently large.
For our purposes we do not wish to detect the spatially random noise,
but rather to avoid it in our thresholded image. We therefore select the
threshold which maximises the relative variance, thereby maximising
``clumpiness'' (regions of change) and minimising the Poisson
distribution (noise).



Next:
6 Modelling the spatial
Up:
Thresholding for Change Detection
Previous:
4 Modelling the signal
Paul L Rosin
Mon Jun 23 08:34:37 BST 1997
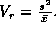 It is calculated by first counting the number of observations (in our
case the number of above threshold pixels in the difference map) in
n
windows,
It is calculated by first counting the number of observations (in our
case the number of above threshold pixels in the difference map) in
n
windows,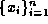 , from which the mean,
, from which the mean,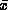 , and variance,
, and variance,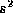 , of the
, of the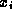 can be found. Although the test is sensitive to the window size and
point density it works adequately as long as
can be found. Although the test is sensitive to the window size and
point density it works adequately as long as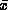 is sufficiently large.
is sufficiently large.

