


Next:
References
Up:
Measuring Corner Properties
Previous:
3 Results
We have described various methods for measuring corner properties. In
order to compare them they have been extensively tested on synthetic
data. This paper presents their average performance. A more detailed
analysis is presented in Rosin [
15
] which helps demonstrate their strengths and weaknesses, and shows
under what conditions each method is suitable. It concludes that some
methods work very well all the time; for instance the thresholding
followed by median and the moments methods consistently measure contrast
better than the multi-scale intensity histogram or thresholding followed
by averaging methods. Other methods perform better than others only over
a restricted range of conditions. For example, in the range of subtended
angles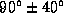 the multi-scale orientation histogram method for measuring subtended
angle outperforms the other methods, but outside this range it breaks
down. Another example is when applying the multi-scale orientation
histogram method to measure corner orientation. Again it outperforms all
the other methods, but breaks down when the SNR drops below 10.
the multi-scale orientation histogram method for measuring subtended
angle outperforms the other methods, but outside this range it breaks
down. Another example is when applying the multi-scale orientation
histogram method to measure corner orientation. Again it outperforms all
the other methods, but breaks down when the SNR drops below 10.
Overall, the average orientation, thresholding, intensity centroid and
all the symmetry methods are all good choices for measuring orientation.
Although it breaks down for very narrow or wide corners the multi-scale
orientation histogram method is probably the best choice for measuring
subtended angle. The thresholding followed by median and the moments
methods are best for measuring contrast. The moments method being more
robust under severe noise or when a small measurement window is used.
A more limited set of tests have been applied to the methods for
measuring bluntness and cusp boundary curvature. For measuring bluntness
the kurtosis and hyperbola fitting methods do better than the circle
fitting method when the corner is substantially rounded. Finally, the
method for measuring boundary shape of cusps appears to work reliably.



Next:
References
Up:
Measuring Corner Properties
Previous:
3 Results
Paul L Rosin
Fri Jun 20 15:42:03 BST 1997
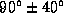 the multi-scale orientation histogram method for measuring subtended
angle outperforms the other methods, but outside this range it breaks
down. Another example is when applying the multi-scale orientation
histogram method to measure corner orientation. Again it outperforms all
the other methods, but breaks down when the SNR drops below 10.
the multi-scale orientation histogram method for measuring subtended
angle outperforms the other methods, but outside this range it breaks
down. Another example is when applying the multi-scale orientation
histogram method to measure corner orientation. Again it outperforms all
the other methods, but breaks down when the SNR drops below 10.

